Solveeit Logo
Login

Question

Question: If two normal to a parabola \[{y^2} = 4ax\] intersect at right angles then the chord joining their f...

If two normal to a parabola y2=4ax{y^2} = 4ax intersect at right angles then the chord joining their feet passes through a fixed point whose coordinates are:
A.(-2a, 0)
B.(a, 0)
C.(2a, 0)
D.None of these.

Explanation

Solution

Hint : To solve this problem we need to know the parameters of parabola. That is x=at2x = a{t^2} and y=2aty = 2at . We find the slope of the two normal lines and using some relation we will obtain the required answer. We know that the equation of parabola y2=4ax{y^2} = 4ax is y=0y = 0 and axis along the positive x-axis.

Complete step-by-step answer :
Given, two normal intersect at right angles and we obtain a chord PQ as shown in the figure.

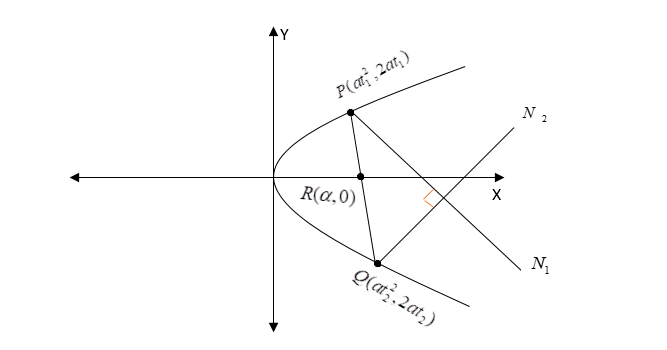
Here we need to find the point R(α,0)R(\alpha ,0) .
Now, using the parametric of parabola we have points: P(at12,2at1)P(at_1^2,2a{t_1}) and Q(at22,2at2)Q(at_2^2,2a{t_2})
We know the slope of the normal is =−t = - t .
Now, the slope of normal at N1=−t1{N_1} = - {t_1} .
Slope of normal at N2=−t2{N_2} = - {t_2} .
We know that if N1⊥N2{N_1} \bot {N_2} their product will be -1.
⇒(−t1)(−t2)=−1\Rightarrow ( - {t_1})( - {t_2}) = - 1
⇒t1t2=−1\Rightarrow {t_1}{t_2} = - 1
⇒t2=−1t1\Rightarrow {t_2} = - \dfrac{1}{{{t_1}}}
Now using this we get P(at12,2at1)P(at_1^2,2a{t_1}) and Q(at12,−2at1)Q\left( {\dfrac{a}{{t_1^2}}, - \dfrac{{2a}}{{{t_1}}}} \right)
From the figure we have that the slope of PR is equal to the slope of PQ.
Also we know slope m=y1−y2x1−x2m = \dfrac{{{y_1} - {y_2}}}{{{x_1} - {x_2}}}
Using the coordinates P(at12,2at1)P(at_1^2,2a{t_1}) R(α,0)R(\alpha ,0) and Q(at22,2at2)Q(at_2^2,2a{t_2}) .
mPR=mPQ{m_{PR}} = {m_{PQ}}
⇒2at1−0at12−α=2at1−2at2at12−at22\Rightarrow \dfrac{{2a{t_1} - 0}}{{at_1^2 - \alpha }} = \dfrac{{2a{t_1} - 2a{t_2}}}{{at_1^2 - at_2^2}}
Taking a common on the right hand side,
⇒2at1−0at12−α=a(2t1−2t2)a(t12−t22)\Rightarrow \dfrac{{2a{t_1} - 0}}{{at_1^2 - \alpha }} = \dfrac{{a(2{t_1} - 2{t_2})}}{{a(t_1^2 - t_2^2)}}
⇒2at1−0at12−α=(2t1−2t2)(t12−t22)\Rightarrow \dfrac{{2a{t_1} - 0}}{{at_1^2 - \alpha }} = \dfrac{{(2{t_1} - 2{t_2})}}{{(t_1^2 - t_2^2)}}
We know a2−b2=(a−b)(a+b){a^2} - {b^2} = (a - b)(a + b)
⇒2at1−0at12−α=2(t1−t2)(t1−t2)(t1+t2)\Rightarrow \dfrac{{2a{t_1} - 0}}{{at_1^2 - \alpha }} = \dfrac{{2({t_1} - {t_2})}}{{({t_1} - {t_2})({t_1} + {t_2})}}
Cancelling the terms,
⇒2at1−0at12−α=2(t1+t2)\Rightarrow \dfrac{{2a{t_1} - 0}}{{at_1^2 - \alpha }} = \dfrac{2}{{({t_1} + {t_2})}}
Cross multiplication,
⇒(2at1−0)(t1+t2)=2(at12−α)\Rightarrow (2a{t_1} - 0)\left( {{t_1} + {t_2}} \right) = 2(at_1^2 - \alpha )
⇒2at12+2at1t2=2at12−2α\Rightarrow 2at_1^2 + 2a{t_1}{t_2} = 2at_1^2 - 2\alpha
Cancelling terms,
⇒−2α=2at1t2\Rightarrow - 2\alpha = 2a{t_1}{t_2}
⇒−α=at1t2\Rightarrow - \alpha = a{t_1}{t_2}
But we have t1t2=−1{t_1}{t_2} = - 1
⇒−α=−a\Rightarrow - \alpha = - a
⇒α=a\Rightarrow \alpha = a
Thus we have R(a,0)R(a,0) .
That is, if two normal to a parabola y2=4ax{y^2} = 4ax intersect at right angles then the chord joining their feet passes through a fixed point whose coordinates are (a,0)(a,0) .
So, the correct answer is “Option B”.

Note : Always try to write the given word problem into a diagram as we did above, it will give us some ideas about what needs to be found. Remember that in this case the slope of tangent 1t\dfrac{1}{t} is and the slope of normal is −t - t . Remember the formula for finding the slopes between two points. Careful about the calculation part.