Question

If two non-parallel lines are perpendicular to two other straight lines, each to each. Show that the acute angle between the first pair of lines is equal to the acute angle between the second pair of lines.

Answer 1

The knowledge of perpendicular and parallel lines is required while solving the problem. We have to further solve it by the acute angle property and then compare the angles which are equal. Hence, we have to draw the diagram carefully to arrive at a conclusion.

Complete step by step answer:

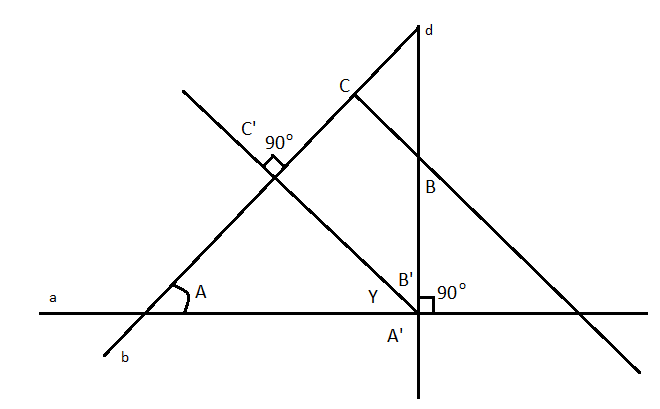
From the above figure we see that:
$A{\kern 1pt}$ and $B$ are two non-perpendicular lines and they are perpendicular to $c$ and $d$
Firstly,
We will move the parallel lines $c$ so as to intersect the point of $\left( A \right)$ intersection of $a$ and $d$ and call it $c'$ Secondly,
As we know $y = (90 - A)$ due to the right-angled triangle is composed of a straight angle.
Consequently, we see that
On the other hand, $B' = B$ since $c$ and $c'$ are parallel and hence by this we can arrive at a conclusion
$B' = 90 - y$
$= 90 - (90 - A)$
$= A$
$A = B'$
Hence, now we can see that the acute angles between the first pair of lines are equal to the acute angle of the second pair of lines.

Additional Information:
Two lines intersecting each other at 90° or a right angle are called perpendicular lines. If two lines are perpendicular to the same line, they're parallel to each other and could by no means intersect. Adjacent facets of a rectangular and a rectangle are usually perpendicular to each other. Aspects of the proper-angled triangle enclosing the right angle are perpendicular to each other.

Note:
An acute angle is an angle that measures between ${90^ \circ }$ and ${0^ \circ }$ , meaning it is smaller than a right angle. The acute angle measures the angle between the perpendicular lines and hence we arrive at our required answer.