Question

If two medians of a triangle are equal, then prove that the triangle is isosceles.

Answer 1

Hint: Consider a triangle ABC with BD and CE as medians. Taking A as origin, write the position vectors of B and C. Write the sides BD and CE in terms of the position vectors of B and C. Equate them and simplify the equation to prove that the length of two sides of the triangles is equal.

Complete step-by-step answer:
We have to prove that if two medians of a triangle are equal, then the triangle is isosceles.
We will consider the triangle $\Delta ABC$ such that BD and CE are medians of the triangle, as shown in the figure.

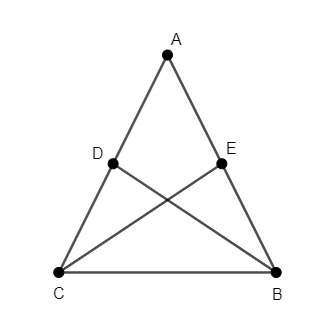
Taking A as origin, we will assume that the position vectors of B and C are $\overset{\to }{\mathop{b}}\,$ and $\overset{\to }{\mathop{c}}\,$ respectively.
As D and E are mid-points of AC and AB, the position vectors of D and E are $\dfrac{\overset{\to }{\mathop{c}}\,}{2}$ and $\dfrac{\overset{\to }{\mathop{b}}\,}{2}$ respectively.
We will now write the position vectors of BD and CE.
We know that in any triangle, the vector sum of two adjacent sides is equal to the vector of the third side.
Thus, in $\Delta ABD$, we have $AD+BD=AB$. We know that $AD=\dfrac{\overset{\to }{\mathop{c}}\,}{2},AB=\overset{\to }{\mathop{b}}\,$.
Thus, we have $\dfrac{\overset{\to }{\mathop{c}}\,}{2}+BD=\overset{\to }{\mathop{b}}\,$.
Rearranging the terms of the above equation, we have $BD=\overset{\to }{\mathop{b}}\,-\dfrac{\overset{\to }{\mathop{c}}\,}{2}.....\left( 1 \right)$.
Similarly, in $\Delta ACE$, we have $AE+CE=AC$. We know that $AE=\dfrac{\overset{\to }{\mathop{b}}\,}{2},AB=\overset{\to }{\mathop{c}}\,$.
Thus, we have $\dfrac{\overset{\to }{\mathop{b}}\,}{2}+CE=\overset{\to }{\mathop{c}}\,$
Rearranging the terms of the above equation, we have $CE=\overset{\to }{\mathop{c}}\,-\dfrac{\overset{\to }{\mathop{b}}\,}{2}.....\left( 2 \right)$.
We know that the length of the medians is equal. So, we have $BD=CE$.
Using equation (1) and (2), we have $\overset{\to }{\mathop{b}}\,-\dfrac{\overset{\to }{\mathop{c}}\,}{2}=\overset{\to }{\mathop{c}}\,-\dfrac{\overset{\to }{\mathop{b}}\,}{2}$.
Squaring the above equation on both sides, we have ${{\left( \overset{\to }{\mathop{b}}\,-\dfrac{\overset{\to }{\mathop{c}}\,}{2} \right)}^{2}}={{\left( \overset{\to }{\mathop{c}}\,-\dfrac{\overset{\to }{\mathop{b}}\,}{2} \right)}^{2}}.....\left( 3 \right)$.
We know that ${{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab$.
Thus, we can rewrite equation (3) as ${{\left( \overset{\to }{\mathop{b}}\, \right)}^{2}}+{{\left( \dfrac{\overset{\to }{\mathop{c}}\,}{2} \right)}^{2}}-2\left( \overset{\to }{\mathop{b}}\, \right)\left( \dfrac{\overset{\to }{\mathop{c}}\,}{2} \right)={{\left( \overset{\to }{\mathop{c}}\, \right)}^{2}}+{{\left( \dfrac{\overset{\to }{\mathop{b}}\,}{2} \right)}^{2}}-2\left( \overset{\to }{\mathop{c}}\, \right)\left( \dfrac{\overset{\to }{\mathop{b}}\,}{2} \right)$.
Simplifying the above equation, we have ${{\left( \overset{\to }{\mathop{b}}\, \right)}^{2}}+\dfrac{{{\left( \overset{\to }{\mathop{c}}\, \right)}^{2}}}{4}={{\left( \overset{\to }{\mathop{c}}\, \right)}^{2}}+\dfrac{{{\left( \overset{\to }{\mathop{b}}\, \right)}^{2}}}{4}$.
Further solving the above equation, we have ${{\left( \overset{\to }{\mathop{b}}\, \right)}^{2}}-\dfrac{{{\left( \overset{\to }{\mathop{b}}\, \right)}^{2}}}{4}={{\left( \overset{\to }{\mathop{c}}\, \right)}^{2}}-\dfrac{{{\left( \overset{\to }{\mathop{c}}\, \right)}^{2}}}{4}$.
Thus, we have $\dfrac{3{{\left( \overset{\to }{\mathop{b}}\, \right)}^{2}}}{4}=\dfrac{3{{\left( \overset{\to }{\mathop{c}}\, \right)}^{2}}}{4}\Rightarrow {{\left( \overset{\to }{\mathop{b}}\, \right)}^{2}}={{\left( \overset{\to }{\mathop{c}}\, \right)}^{2}}$.
Taking square root on both sides, we have $\overset{\to }{\mathop{c}}\,=\overset{\to }{\mathop{b}}\,$. Thus, we have $AC=AB$.
Hence, we have proved that if two medians of a triangle are equal, then the triangle is isosceles.

Note: We can also solve this question by writing the coordinates of vertices of the triangle and then writing the coordinates of D and E using the midpoint formula. Then use the distance formula to calculate the length of medians and equate them to prove that two sides of the triangle are equal.