Question
Question: If two distinct chords of parabola \[{{y}^{2}}=4ax\], passing through \[\left( a,2a \right)\] are bi...
If two distinct chords of parabola y2=4ax, passing through (a,2a) are bisected on the line x+y=1, then the length of latus rectum is
(a) 2
(b) 1
(c) 4
(d) 5
Solution
The figure showing the given data is
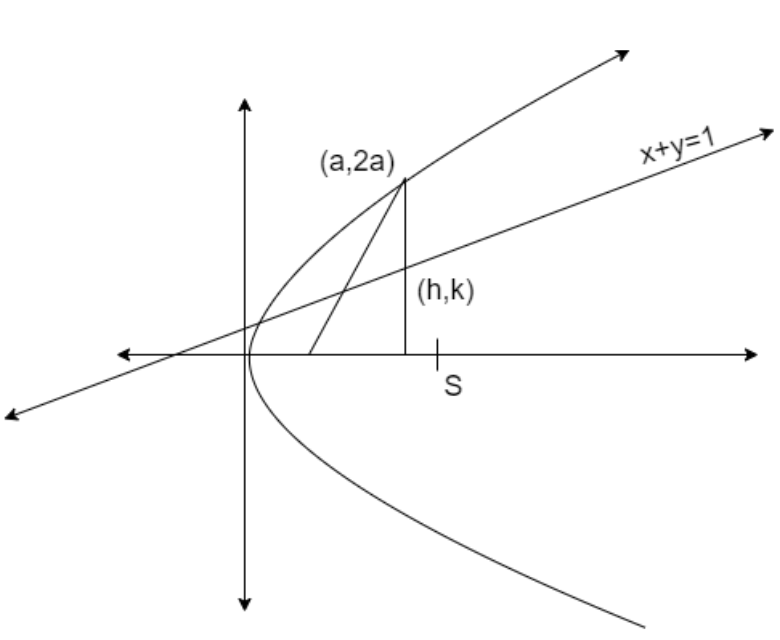
We solve this problem by assuming the mid - point as (h,k) that lies on the line x+y=1. Then we use the formula of the line equation having the mid – point of a curve Sthat is S1=S11. If S≡y2−4ax=0 then the representation S1,S11 with respect to point (x1,y1) is given as
⇒S1=yy1−2a(x+x1)
⇒S11=y12−4ax1
By using the above results we find the range of ′a′ to get the latus rectum as ′4a′
Complete step-by-step solution:
Let us assume that the point at which the chords are bisected as (h,k)
We are given that the chords are bisected on the line x+y=1
We know that the point (h,k) satisfies the equation x+y=1
Now, by substituting the point in the line we get
