Question
Question: If two distinct chords, drawn from the point \[\left( {p,q} \right)\] on the circle \[{x^2} + {y^2} ...
If two distinct chords, drawn from the point (p,q) on the circle x2+y2=px+qy. Given that: pq=0 are bisected by the x-axis, then
A. p2<8q2
B. p2>8q2
C. Cannot be determined
D. None of these
Solution
The given problem revolves around the concepts of geometry. Keeping in mind, first of all, drawing the rough figure/construction from the given data; finding the coordinates of the other end of the respective distinct chord (using the midpoint formula, (x,y)=(2x1+x2,2y1+y2)). As a result, consider the given equation of the circle i.e. x2+y2=px+qy and then substitute the coordinates in that equation. Then, by the condition given i.e. pq=0, using the condition of discrimination such as b2−4ac>0, etc., the desire solution is obtained.
Complete step by step answer:
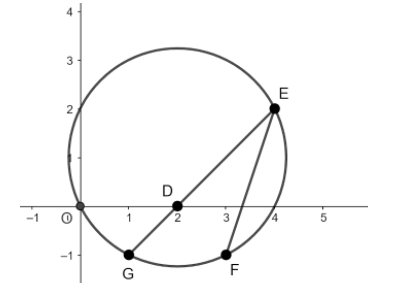
Let us assume the rough figure as drawn above from the respective given data which seems that,
E≡(p,q)≡(x1,y1)
As we have given that it exists two distinct chords that is ‘EG’ and ‘EF’ in the above figure,
Hence, from the construction of the figure it is observed that point ‘D’ is the midpoint of the chord ‘EG’ as it bisects the x-axis,
So,
Let us consider the coordinates of point ‘D’ as,
D≡(g,0)
Where, ‘g’ is the coordinate due to on x-axis i.e. x=g, and
‘0’ no point exists on y-axis i.e. y=0.
Hence, we can now find the coordinates of point ‘G’ from the midpoint formula i.e. (x,y)=(2x1+x2,2y1+y2) as ‘D’ is the midpoint of ‘EG’, we get
⇒(g,0)=(2p+x2,2q+y2) … (Where, x2,y2 are the coordinates of point ‘G’)
Now, equating the equation x-coordinates mathematically, that is
g=2p+x2
2g=p+x2
Hence, x2=2g−p
Similarly,
Equating the y-coordinates, we get
0=2q+y2
0=q+y2
Hence, y2=−q
The coordinates of point ‘G’ on chord ‘EG’ is,
G≡(2g−p,−q)
Now,
Since, considering the given equation (of the circle)
⇒x2+y2=px+qy
Hence, as the point ‘G’ exists from these distinct point i.e. (p,q)
Substituting the values of x=x2=2g−p and y=y2=−q in the equation as the coordinates i.e. x1=p and y1=q, we get
⇒(2g−p)2+(−q)2=p(2g−p)+q(−q)
Solving the equation algebraically, we get
⇒4g2−4gp+p2+q2=2pg−p2−q2 … [∵(a−b)2=a2−2ab+b2]
⇒4g2−4gp+p2+q2−2pg+p2+q2=0
Simplifying the equation, we get
⇒4g2−6pg+2(p2+q2)=0
⇒2g2−3pg+(p2+q2)=0 … (i)
Since, given that pq=0 which seems to be real that is they are the coordinates
Hence, considering ‘g’ as the variable in the above equation
We know that the discriminant for real numbers is,
⇒b2−4ac>0
Hence, substituting the values from the equation (i), we get
(−3p)2−4×2×(p2+q2)>0
9p2−8(p2+q2)>0
Solving the equation predominantly, we get
9p2−8p2−8q2>0
p2−8q2>0
Hence, the required solution is
⇒p2>8q2
So, the correct answer is “Option B”.
Note:
The given problem can be solved similarly by considering any one of the distinct chords (among two) by the same coordinates given i.e. (p,q). One must able to know all the discrimination conditions that is b2−4ac>0, b2−4ac<0, b2−4ac=0 which seems the condition for real, imaginary and the exact solution respectively, so as to be sure of our final answer.
