Question

If two concentric ellipses are such that the foci of one be on the other and their major axes are equal. Let${e_1}$ and ${e_2}$be their eccentricities. Then
The quadrilateral formed by joining the foci of the two ellipses is a parallelogram
Then angle $\theta$ between their axes is given by $\cos \theta = \sqrt {\dfrac{1}{{{e_1}^2}} + \dfrac{1}{{{e_2}^2}} - \dfrac{1}{{{e_1}^2{e_2}^2}}}$
If ${e_1}^2 + {e_2}^2 = 1$ then the angle between the axes of the two ellipses is ${90^0}$
The area of the quadrilateral $= {a^2}\sqrt {{e_1}^2 + {e_2}^2 + {e_1}^2{e_2}^2 - 1}$

Answer 1

Here we have to use the basic equation and concept of ellipse to check whether which statement is true. Firstly we will check whether the quadrilateral formed by joining the foci of the two ellipses is a parallelogram or not by using the length of the major axis. Then we will find the value of $\cos \theta$ to check whether the statement B is true or not. Then we will be able to conclude which options are correct.

Complete step by step solution:
Here, we have to assume that ${\rm{S}}$,${\rm{S'}}$ be the foci of one ellipse and ${\rm{H}}$,${\rm{H'}}$ be the foci of the other ellipse and C is the common center of both the ellipse.

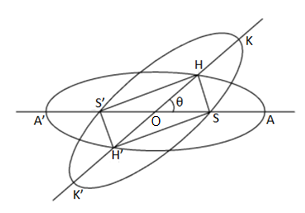
From this we can clearly see that${\rm{SHS'H'}}$ is a parallelogram because${\rm{SH + S'H}} = {\rm{HS'}} + {\rm{H'S'}} = 2a$as the sum of the focal distances of any point on an ellipse is equal to its major axis i.e. $2a$.
Hence, option A is correct.
Now we will find out the value of $\cos \theta$ to check if the option B is correct or not.
Let $\theta$ be the angle between the two ellipses and now we have to assume the value of${\rm{OS}}$and${\rm{OH}}$.
Let ${\rm{OS}} = a{e_1}$ and ${\rm{OH}} = a{e_2}$
Let the equation of ellipse one ${\rm{AA'}}$ be $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b_1}^2}} = 1$.
Let the equation of ellipse two ${\rm{KK'}}$ be $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b_2}^2}} = 1$.
Also we know the value of ${b_1}$ and ${b_2}$. So,
$\Rightarrow {b_1}^2 = {a^2}(1 - {e_1}^2)$
$\Rightarrow {b_2}^2 = {a^2}(1 - {e_2}^2)$
Now we can clearly see that the coordinates of the point H is $\left( {a{e_2}\cos \theta ,a{e_2}\sin \theta } \right)$ . The point H lies on the ellipse one i.e. ${\rm{AA'}}$. Therefore it will satisfy the equation of the ellipse one. So, we get
$\Rightarrow \dfrac{{{{\left( {a{e_2}\cos \theta } \right)}^2}}}{{{a^2}}} + \dfrac{{{{\left( {a{e_2}\sin \theta } \right)}^2}}}{{{b_1}^2}} = 1$
Substituting the value of ${b_1}^2$ in the above equation, we get
$\Rightarrow \dfrac{{{{\left( {a{e_2}\cos \theta } \right)}^2}}}{{{a^2}}} + \dfrac{{{{\left( {a{e_2}\sin \theta } \right)}^2}}}{{{a^2}(1 - {e_1}^2)}} = 1$
Simplifying the equation, we get
$\Rightarrow \dfrac{{{a^2}{e_2}^2{{\cos }^2}\theta }}{{{a^2}}} + \dfrac{{{a^2}{e_2}^2{{\sin }^2}\theta }}{{{a^2}(1 - {e_1}^2)}} = 1$
$\Rightarrow {e_2}^2{\cos ^2}\theta + \dfrac{{{e_2}^2{{\sin }^2}\theta }}{{1 - {e_1}^2}} = 1$
Now we will use the trigonometric identity to convert the ${\sin ^2}\theta$ in terms of ${\cos ^2}\theta$. So the identity used is ${\sin ^2}\theta + {\cos ^2}\theta = 1$. So, from this identity we get${\sin ^2}\theta = 1 - {\cos ^2}\theta$.
Therefore the above equation becomes,
$\Rightarrow {e_2}^2{\cos ^2}\theta + \dfrac{{{e_2}^2\left( {1 - {{\cos }^2}\theta } \right)}}{{1 - {e_1}^2}} = 1$
Simplifying the equation we get
$\Rightarrow {\cos ^2}\theta \left( {{e_2}^2 - \dfrac{{{e_2}^2}}{{1 - {e_1}^2}}} \right) = \left( {1 - \dfrac{{{e_2}^2}}{{1 - {e_1}^2}}} \right)$
Now we will find the value of $\cos \theta$ by the above equation by simplifying the equation. So, we get
$\Rightarrow {\cos ^2}\theta \left( {\left( {1 - {e_1}^2} \right){e_2}^2 - {e_2}^2} \right) = \left( {1 - {e_1}^2 - {e_2}^2} \right)$
$\Rightarrow {\cos ^2}\theta = \dfrac{{\left( {1 - {e_1}^2 - {e_2}^2} \right)}}{{\left( {\left( {1 - {e_1}^2} \right){e_2}^2 - {e_2}^2} \right)}}$
$\Rightarrow \cos \theta = \sqrt {\dfrac{{\left( {1 - {e_1}^2 - {e_2}^2} \right)}}{{\left( {\left( {1 - {e_1}^2} \right){e_2}^2 - {e_2}^2} \right)}}}$
Now by simplifying the above equation, we get
$\Rightarrow \cos \theta = \sqrt {\dfrac{{\left( {{e_1}^2 + {e_2}^2 - 1} \right)}}{{\left( {{e_1}^2{e_2}^2} \right)}}}$
Or we can write it as $\cos \theta = \sqrt {\dfrac{1}{{{e_1}^2}} + \dfrac{1}{{{e_2}^2}} - \dfrac{1}{{{e_1}^2{e_2}^2}}}$

Hence, both the option A and option B is correct.

Note:
Here we have to keep in mind that in case of an ellipse the sum of the focal distances of any point on an ellipse is equal to its major axis. Ellipse is an oval type shape which has a minor and major axis. We should know the general equation of the ellipse i.e. $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$ where, $a$ is the distance of the end of major axis from the center and $b$ is the distance of the end of minor axis from the center.
We should know that if any curve or line passes through a point then the value of the coordinate of the point always satisfies the equation of the curve.