Question

If two circles intersect at two points, prove that their centre lies on the perpendicular bisector of the common chord.

Answer 1

Hint- Here we will proceed by the construction of perpendicular. Then, we will prove that the triangles are congruent so as to prove that their centres lie on the perpendicular bisector of the common chord.

Complete step-by-step answer:

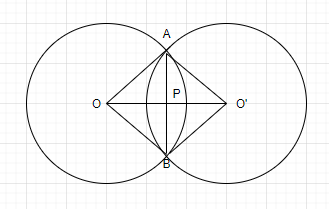
Given – Two circles, with centre O and O’ intersect at two points A and B. AB is the common chord of the two circles and OO’ is the line segment joining the centres of the two circles. Let OO’ intersect AB at P.
To prove: $OO'$ is the perpendicular bisector of AB.
Construction: Join, $OA,{\text{ OB, O'A }}$and $O'B$
Proof: In triangles $OAO'$ and $OBO'$ , we have
$OO' = OO'$ (Common)
$OA = OB$ (Radii of the same circle)
$O'A = O'B$ (Radii of the same circle)
$\Rightarrow \Delta OAO' \cong \Delta OBO'$ (SSS congruence criterion)
$\Rightarrow < AOO' = < BOO'$ (Corresponding part of the congruent triangle)
That is, $< AOP = < BOP$
In triangles $AOP$ and $BOP$, we have
$OP = OP$ (Common)
$< AOP = < BOP$ (Proved above)
$OA = OB$ (Radii of the same circle)
$\therefore \Delta AOP = \Delta BOP$ (By side angle side congruence criterion)
$\Rightarrow AP = BP$ (Corresponding part of congruent triangle)
But
$< APO + < APO’ = {180^ \circ } \\\ \Rightarrow 2 < APO = {180^ \circ } \\\ \Rightarrow {\text{ }} < APO = {90^ \circ } \\\$
Thus, $AP = BP{\text{ and < APO = < BPO = }}{90^ \circ }$
Hence, OO’ is the perpendicular bisector of $AB$.

Note:Whenever we come up with this type of problem, one should know that the point of contact of two circles will lie on the line joining the centres of the two circles such that sum or difference of the radii of the circles will equal the distance between the centres of the circles depending upon whether the circles touch externally or internally.