Question

If two bulbs of $25\;{{W}}$ and $100\;{{W}}$ rated at $200\,V$ are connected in $440\,V$ supply, then
(A) $100$ watt bulb will fuse
(B) $25$ watt bulb will fuse
(C) none of the bulb will fuse
(D) both the bulbs will fuse

Answer 1

The resistance of each bulb will be different hence they have different powers. The voltage across each bulb has to be found using the resistance. Then the result will be compared to the voltage rating of the bulbs. By using the formula of the power, then the solution will be determined.

Complete step by step solution:
Given two bulbs having power, ${P_1} = 25\;{{W}}$ and ${P_2} = 100\;{{W}}$both are rated at voltage, $V = 200\;{{volts}}$ and connected in series with $440$ volts supply.

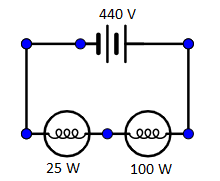
The expression for power is given as,
$P = \dfrac{{{V^2}}}{R}$
Where, $V$ is the voltage and $R$ is the resistance.
From the above expression,
$R = \dfrac{{{V^2}}}{P}$
Hence, we can find the resistance of each bulb using this equation for the given power and voltage rating.
$\Rightarrow {R_1} = \dfrac{{{V^2}}}{{{P_1}}} \\\ \Rightarrow \dfrac{{{{\left( {200\;{{V}}} \right)}^2}}}{{25\;{{W}}}} \\\ \Rightarrow 1600\;\Omega$
The resistance of $25\;{{W}}$ bulb is $1600\;\Omega$.
And,
$\Rightarrow {R_2} = \dfrac{{{V^2}}}{{{P_2}}} \\\ \Rightarrow \dfrac{{{{\left( {200\;{{V}}} \right)}^2}}}{{100\;{{W}}}} \\\ \Rightarrow 400\;\Omega$
The resistance of $100\;{{W}}$ is $400\;\Omega$.
Since the two bulbs are connected in series, the total resistance will be ${R_1} + {R_2}$.
The voltage across each bulb will be different. They are connected to $440$ volts supply also.
Hence, the voltage across the $25\;{{W}}$ bulb is given as,
$\Rightarrow {V_1} = 440\;{{V}} \times \dfrac{{{R_1}}}{{{R_1} + {R_2}}}$
Substituting the values in the above expression,
$\Rightarrow {V_1} = 440\;{{V}} \times \dfrac{{1600\;\Omega }}{{1600\;\Omega + 400\;\Omega }} \\\ \Rightarrow 352\;{{V}}$
The voltage across $25\;{{W}}$ is $352\;{{V}}$. This is higher than the rated voltage $200\;{{volts}}$. Therefore, the bulb will fuse.
The voltage across $100\;{{W}}$ bulb is given as,
$\Rightarrow {V_2} = 440\;{{V}} \times \dfrac{{{R_2}}}{{{R_1} + {R_2}}}$
Substituting the values in the above expression,
$\Rightarrow {V_2} = 440\;{{V}} \times \dfrac{{400\;\Omega }}{{1600\;\Omega + 400\;\Omega }} \\\ \Rightarrow 88\;{{V}}$
The voltage across $100\;{{W}}$ is $88\;{{V}}$. This is lower than the rated voltage $200\;{{volts}}$. Therefore, the bulb will not fuse.
Therefore, only the $25\;{{W}}$ bulb will fuse.

The answer is option B.

Note: If two bulbs have the same voltage rating but the power is different, then a bulb having high power will have low resistance. And the low power bulb will fuse than the high power bulb. The power is directly proportional to the square of the voltage and inversely proportional to the resistance.