Solveeit Logo
Login

Question

Question: If $\triangle ABC$ and $\triangle AEF$ are such that EB = BF, AB = EF = 1, BC = 6, AC = $\sqrt{33}$ ...

If △ABC\triangle ABC and △AEF\triangle AEF are such that EB = BF, AB = EF = 1, BC = 6, AC = 33\sqrt{33} and AB‾.AE‾+AC‾.AF‾\overline{AB}.\overline{AE}+\overline{AC}.\overline{AF} = 2, then the value of BC‾.BF‾\overline{BC}.\overline{BF} is (given figure)

Answer

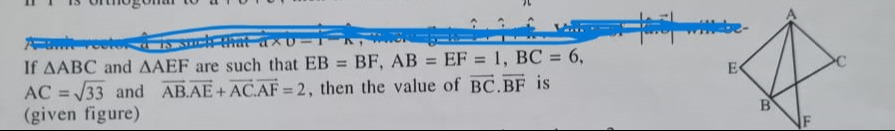
2

Explanation

Solution

Let A be the origin. Let the position vectors of points B, C, E, F be b⃗,c⃗,e⃗,f⃗\vec{b}, \vec{c}, \vec{e}, \vec{f} respectively.
We are given AB = ∣b⃗∣=1|\vec{b}| = 1, BC = ∣c⃗−b⃗∣=6|\vec{c} - \vec{b}| = 6, AC = ∣c⃗∣=33|\vec{c}| = \sqrt{33}, EF = ∣f⃗−e⃗∣=1|\vec{f} - \vec{e}| = 1.
We are given that EB = BF, which means B is the midpoint of the line segment EF. Thus, the position vector of B is the average of the position vectors of E and F: b⃗=e⃗+f⃗2\vec{b} = \frac{\vec{e} + \vec{f}}{2}, which implies e⃗+f⃗=2b⃗\vec{e} + \vec{f} = 2\vec{b}.

We are given the equation AB‾.AE‾+AC‾.AF‾=2\overline{AB}.\overline{AE}+\overline{AC}.\overline{AF} = 2. In terms of position vectors relative to A, this is b⃗.e⃗+c⃗.f⃗=2\vec{b}.\vec{e} + \vec{c}.\vec{f} = 2.

We want to find the value of BC‾.BF‾\overline{BC}.\overline{BF}.
BC‾=c⃗−b⃗\overline{BC} = \vec{c} - \vec{b}.
BF‾=f⃗−b⃗\overline{BF} = \vec{f} - \vec{b}.
So, BC‾.BF‾=(c⃗−b⃗).(f⃗−b⃗)=c⃗.f⃗−c⃗.b⃗−b⃗.f⃗+b⃗.b⃗\overline{BC}.\overline{BF} = (\vec{c} - \vec{b}).(\vec{f} - \vec{b}) = \vec{c}.\vec{f} - \vec{c}.\vec{b} - \vec{b}.\vec{f} + \vec{b}.\vec{b}.

From e⃗+f⃗=2b⃗\vec{e} + \vec{f} = 2\vec{b}, we have e⃗=2b⃗−f⃗\vec{e} = 2\vec{b} - \vec{f}.
Substitute this into the equation b⃗.e⃗+c⃗.f⃗=2\vec{b}.\vec{e} + \vec{c}.\vec{f} = 2:
b⃗.(2b⃗−f⃗)+c⃗.f⃗=2\vec{b}.(2\vec{b} - \vec{f}) + \vec{c}.\vec{f} = 2
2b⃗.b⃗−b⃗.f⃗+c⃗.f⃗=22\vec{b}.\vec{b} - \vec{b}.\vec{f} + \vec{c}.\vec{f} = 2
2∣b⃗∣2−b⃗.f⃗+c⃗.f⃗=22|\vec{b}|^2 - \vec{b}.\vec{f} + \vec{c}.\vec{f} = 2
Since ∣b⃗∣=AB=1|\vec{b}| = AB = 1, we have 2(1)2−b⃗.f⃗+c⃗.f⃗=22(1)^2 - \vec{b}.\vec{f} + \vec{c}.\vec{f} = 2.
2−b⃗.f⃗+c⃗.f⃗=22 - \vec{b}.\vec{f} + \vec{c}.\vec{f} = 2.
−b⃗.f⃗+c⃗.f⃗=0-\vec{b}.\vec{f} + \vec{c}.\vec{f} = 0.
f⃗.(c⃗−b⃗)=0\vec{f}.(\vec{c} - \vec{b}) = 0.
This means f⃗.BC‾=0\vec{f}.\overline{BC} = 0, or AF‾⊥BC‾\overline{AF} \perp \overline{BC}.

Now substitute c⃗.f⃗=b⃗.f⃗\vec{c}.\vec{f} = \vec{b}.\vec{f} into the expression for BC‾.BF‾\overline{BC}.\overline{BF}:
BC‾.BF‾=b⃗.f⃗−c⃗.b⃗−b⃗.f⃗+∣b⃗∣2=−c⃗.b⃗+1\overline{BC}.\overline{BF} = \vec{b}.\vec{f} - \vec{c}.\vec{b} - \vec{b}.\vec{f} + |\vec{b}|^2 = -\vec{c}.\vec{b} + 1.

We need to find the value of c⃗.b⃗\vec{c}.\vec{b}.
c⃗.b⃗=∣c⃗∣∣b⃗∣cos⁡(∠CAB)\vec{c}.\vec{b} = |\vec{c}||\vec{b}| \cos(\angle CAB).
In △ABC\triangle ABC, by the Law of Cosines, BC2=AB2+AC2−2AB⋅ACcos⁡(∠CAB)BC^2 = AB^2 + AC^2 - 2 AB \cdot AC \cos(\angle CAB).
We are given BC = 6, AB = 1, AC = 33\sqrt{33}.
62=12+(33)2−2(1)(33)cos⁡(∠CAB)6^2 = 1^2 + (\sqrt{33})^2 - 2 (1)(\sqrt{33}) \cos(\angle CAB).
36=1+33−233cos⁡(∠CAB)36 = 1 + 33 - 2\sqrt{33} \cos(\angle CAB).
36=34−233cos⁡(∠CAB)36 = 34 - 2\sqrt{33} \cos(\angle CAB).
233cos⁡(∠CAB)=34−36=−22\sqrt{33} \cos(\angle CAB) = 34 - 36 = -2.
cos⁡(∠CAB)=−2233=−133\cos(\angle CAB) = \frac{-2}{2\sqrt{33}} = -\frac{1}{\sqrt{33}}.

Now, c⃗.b⃗=∣c⃗∣∣b⃗∣cos⁡(∠CAB)=33×1×(−133)=−1\vec{c}.\vec{b} = |\vec{c}||\vec{b}| \cos(\angle CAB) = \sqrt{33} \times 1 \times \left(-\frac{1}{\sqrt{33}}\right) = -1.

Finally, BC‾.BF‾=−c⃗.b⃗+1=−(−1)+1=1+1=2\overline{BC}.\overline{BF} = -\vec{c}.\vec{b} + 1 = -(-1) + 1 = 1 + 1 = 2.