Question

If three of the six vertices of a regular hexagon are chosen at random, then the probability that the triangle formed with these chosen vertices is equilateral is?
A. $\dfrac{3}{10}$
B. $\dfrac{1}{10}$
C. $\dfrac{3}{20}$
D. $\dfrac{1}{5}$

Answer 1

We will first draw a hexagon and then find the total number of outcomes by finding the number of ways of choosing 3 points to form a triangle from the given 6 points. We will then find the total number of favorable outcomes by finding the total number of equilateral triangles. Hence, we will find the probability by dividing the number of favorable outcomes by the number of total outcomes.

Complete step-by-step solution:
In the given question, we are asked to find the probability of choosing three out of six vertices of a hexagon that can form the vertices of an equilateral triangle. Before proceeding, let us first find out about probability. Probability is that branch of mathematics that concerns the numerical description of how likely an event can occur or how likely is that a proposition is true. A simple example is the tossing of a fair or unbiased coin. Here the probability of an event is the number between 0 and 1, where we can say roughly, 0 indicates the impossibility, and 1 indicates the certainty of the event. The higher the probability of an event, the more likely it is that the event will occur. Since the coin is a fair coin, the two outcome, ‘heads’ and ‘tails’ are both equally probable; the probability of ‘heads’ is equal to the probability of ‘tails’ and since there are no other outcomes possible, the probability of either ‘heads’ or ‘tails’ is given by $\dfrac{1}{2}$. We find the probability by using a general formula, $P\left( E \right)=\dfrac{n\left( F \right)}{n\left( E \right)}$ , where $P\left( E \right)$ represents the probability of the event, $n\left( F \right)$ represents the number of favourable outcomes of the event and $n\left( E \right)$ represents the total number of outcomes of the events.
In this given question, let us assume the hexagon as ABCDEF as shown in the figure below.

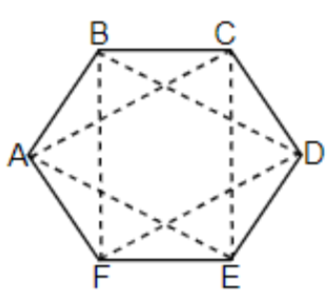
As we can see from the figure, there are only two triangles possible which are equilateral in nature. So, the number of favourable outcomes or $n\left( F \right)$ will be 2. Now, the total number of outcomes, $n\left( E \right)$ will be the total number of ways of choosing 3 points from the 6 vertices, which can be done in ${}^{6}{{C}_{3}}$ ways. To find the ${}^{6}{{C}_{3}}$ ways, we will use the formula given by, ${}^{n}{{C}_{r}}=\dfrac{n!}{r!\left( n-r \right)!}$, so we get it as,
$\begin{aligned} & {}^{6}{{C}_{3}}=\dfrac{6!}{3!\left( 6-3 \right)!} \\\ & \Rightarrow {}^{6}{{C}_{3}}=\dfrac{6!}{3!\times 3!} \\\ & \Rightarrow {}^{6}{{C}_{3}}=\dfrac{6\times 5\times 4\times 3!}{3!\times 3!} \\\ & \Rightarrow {}^{6}{{C}_{3}}=\dfrac{6\times 5\times 4}{3\times 2\times 1} \\\ & \Rightarrow {}^{6}{{C}_{3}}=2\times 5\times 2 \\\ & \Rightarrow {}^{6}{{C}_{3}}=20 \\\ \end{aligned}$
Thus, we get the value of $n\left( E \right)$ as 20. So, we can get the probability as,
$\begin{aligned} & P\left( E \right)=\dfrac{n\left( F \right)}{n\left( E \right)} \\\ & \Rightarrow P\left( E \right)=\dfrac{2}{20} \\\ & \Rightarrow P\left( E \right)=\dfrac{1}{10} \\\ \end{aligned}$
Hence, the correct answer is option B.

Note: While calculating probability, the students generally tend to miss out on the favorable outcome or do make mistakes while calculating the total number of outcomes which leads to a wrong answer. So, they should be careful. Here for the given problem n(E) is the number of selecting 3 vertices out of 6 given vertices of hexagon and n(F) is the number of equilateral triangles so do not confuse b/w n(E) and n(F).