Question

If this dipole were kept in a uniform external electric field${E_0}$​, diagrammatically represent the position of the dipole in stable and unstable equilibrium and write the expressions for the torque acting on the dipole in both cases.

Answer 1

Hint In this question, the dipole is kept in a uniform electric field. And we have to write the expressions for them in two different cases. So for solving this, we will keep the dipole at two positions and then, will find the dipole at $\theta = {0^ \circ }$ and at$\theta = {180^0}$.
Formula used:
The potential energy of the dipole will be equal to the
$U = - P{E_0}\cos \theta$
And for torque, the formula will be
$\tau = P{E_0}\sin \theta$
Here,
$U$, will be the potential energy of the dipole
$\tau$ , will be the torque
$P$, will be the electric dipole of the dipole moment
${E_0}$, will be the uniform electric field

Complete Step By Step Solution Let us assume that the dipole we are using is kept at two positions namely $\left( a \right)$ and $\left( b \right)$ which is placed in a constant electric field ${E_0}$ as it is shown in the below diagram.

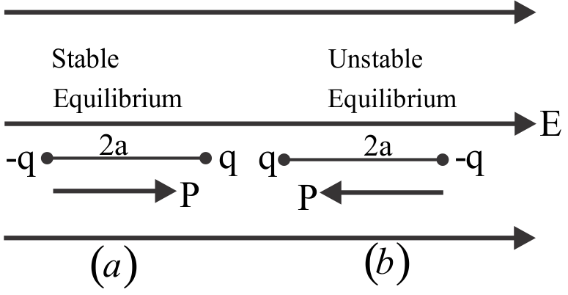
In the first case: When the angle between the dipole and electric field will be zero
Then, the Potential energy of the dipole will be equal to the
$U = - P{E_0}\cos \theta$
Therefore,
$\Rightarrow U = - P{E_0}\cos {0^ \circ }$
And on simplifying the equation, we get
Since $\cos {0^ \circ } = 1$
$\Rightarrow U = - P{E_0}$
Therefore, we can say that the dipole will be in stable equilibrium.
Now we will find the torque,
And for torque, the formula will be
$\tau = P{E_0}\sin \theta$
$\Rightarrow \tau = P{E_0}\sin {0^0}$
$\Rightarrow \tau = 0$
In the second case: When the angle between the dipole and electric field will be ${180^ \circ }$
Then, the Potential energy of the dipole will be equal to the
$U = - P{E_0}\cos \theta$
Therefore,
$\Rightarrow U = - P{E_0}\cos {180^ \circ }$
And on simplifying the equation, we get
Since $\cos {180^ \circ } = - 1$
$\Rightarrow U = P{E_0}$
Therefore, we can say that the dipole will be in unstable equilibrium.
Now we will find the torque,
And for torque, the formula will be
$\tau = P{E_0}\sin \theta$
$\Rightarrow \tau = P{E_0}\sin {180^0}$
$\therefore \tau = 0$

Note Stable equilibrium means the lowest potential energy at the equilibrium point. Therefore the stable equilibrium the torque should be zero and the potential energy of the dipole should be minimum. Whereas the unstable equilibrium torque will be zero and the potential energy should be maximum or positive.