Question

If $\theta$ is the semi-vertical angle of a cone of maximum volume and given slant height, then $\tan \theta$ is given by:
(a) 2
(b) 1
(c) $\sqrt{2}$
(d) $\sqrt{3}$

Answer 1

Hint:In this question, we first need to write the base radius and height of the cone in terms of its slant height and semi vertical angle. Then substitute these values in the volume of the cone formula and differentiate it and equal to 0 to get the result.
$V=\dfrac{1}{3}\pi {{r}^{2}}h$

Complete step-by-step answer:
Right Circular Cone:
A right circular cone is a solid generated by revolving of a right angled triangle through one of its sides (other than hypotenuse) containing the right angle as an axis.
Volume of a cone is given by the formula
$V=\dfrac{1}{3}\pi {{r}^{2}}h$

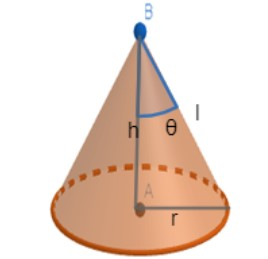
Let us assume that the slant height of the cone as l, base radius as r and height of the cone as h.
Now, the base radius can be written in terms of slant height and semi vertical angle as
$\Rightarrow r=l\sin \theta$
Now, the height of the cone can be written in terms of slant height and semi vertical angle as
$\Rightarrow h=l\cos \theta$
Now, by substituting these in the volume of a cone formula we get,

& \Rightarrow V=\dfrac{1}{3}\pi {{r}^{2}}h \\\ & \Rightarrow V=\dfrac{1}{3}\pi \times {{\left( l\sin \theta \right)}^{2}}\times l\cos \theta \\\ \end{aligned}$$ Now, on further simplifying the terms we get, $$\Rightarrow \dfrac{1}{3}\pi \times {{l}^{3}}\times {{\sin }^{2}}\theta \times \cos \theta $$ Now, let us write the sine terms in cosine terms. $$\Rightarrow \dfrac{1}{3}\pi \times {{l}^{3}}\times \left( 1-{{\cos }^{2}}\theta \right)\times \cos \theta $$ Now, this can be further written as $$\Rightarrow V=\dfrac{1}{3}\pi \times {{l}^{3}}\times \left( \cos \theta -{{\cos }^{3}}\theta \right)$$ Given in the question that the volume of the cone is maximum. $$\begin{aligned} & \Rightarrow \dfrac{dV}{d\theta }=0 \\\ & \Rightarrow \dfrac{d}{d\theta }\left( \dfrac{1}{3}\pi \times {{l}^{3}}\times \left( \cos \theta -{{\cos }^{3}}\theta \right) \right)=0 \\\ \end{aligned}$$ This can be further written as $$\Rightarrow \dfrac{1}{3}\pi \times {{l}^{3}}\times \left( -\sin \theta -3{{\cos }^{2}}\theta \times \left( -\sin \theta \right) \right)=0$$ As the other terms are constant and cannot be equal to zero we can now write it as $$\Rightarrow -\sin \theta -3{{\cos }^{2}}\theta \times \left( -\sin \theta \right)=0$$ Now, on rearranging the terms we get, $$\Rightarrow 3{{\cos }^{2}}\theta \times \sin \theta =\sin \theta $$ Let us now cancel out the common and simplify it further. $$\Rightarrow 3{{\cos }^{2}}\theta =1$$ Now, by dividing with 3 on both sides and applying square root we get, $$\therefore \cos \theta =\dfrac{1}{\sqrt{3}}$$ As we already know that $$\begin{aligned} & \cos \theta =\dfrac{\text{adjacent}}{\text{Hypotenuse}} \\\ & \tan \theta =\dfrac{\text{Opposite}}{\text{adjacent}} \\\ \end{aligned}$$ Now, opposite side can be calculated by $$\begin{aligned} & \Rightarrow \sqrt{{{\left( \sqrt{3} \right)}^{2}}-1} \\\ & \Rightarrow \sqrt{3-1} \\\ & \Rightarrow \sqrt{2} \\\ \end{aligned}$$ $$\begin{aligned} & \Rightarrow \tan \theta =\dfrac{\sqrt{2}}{1} \\\ & \therefore \tan \theta =\sqrt{2} \\\ \end{aligned}$$ Hence, the correct option is (c). Note:While doing the differentiation instead of converting the sine terms into cosine we can just apply the u v formula to expand the differentiation and then equate it to zero. Both the methods give the same result. Instead of finding the opposite side we can get the value of sine from cosine by using trigonometric identity. Then dividing the sine value with cosine value gives the tangent values. Here, also the answer will be the same.