Question

If $\theta$ is an acute angle and $\sin \dfrac{\theta }{2}=\sqrt{\dfrac{x-1}{2x}}$, then $\tan \theta$ is equal to
A. ${{x}^{2}}-1$
B. $\sqrt{{{x}^{2}}-1}$
C. $\sqrt{{{x}^{2}}+1}$
D. ${{x}^{2}}+1$

Answer 1

We first use the multiple angle formula $\cos \theta =1-2{{\sin }^{2}}\dfrac{\theta }{2}$ to find the value of $\cos \theta$. We use the representation of a right-angle triangle with base and hypotenuse ratio being $\dfrac{1}{x}$ and the angle being $\theta$. We also take the trigonometric ratio formula to find the value of $\tan \theta$.

Complete step by step answer:
It is given that $\theta$ is an acute angle and $\sin \dfrac{\theta }{2}=\sqrt{\dfrac{x-1}{2x}}$.
From the multiple angle formula we know that $\cos \theta =1-2{{\sin }^{2}}\dfrac{\theta }{2}$.
We put the values to get $\cos \theta =1-2{{\left( \sqrt{\dfrac{x-1}{2x}} \right)}^{2}}=1-\dfrac{x-1}{x}=\dfrac{1}{x}$.
We know $\cos \theta =\dfrac{\text{base}}{\text{hypotenuse}}$. We can take the representation of a right-angle triangle with base and hypotenuse ratio being $\dfrac{1}{x}$ and the angle being $\theta$. The height and base were considered with respect to that particular angle $\theta$.

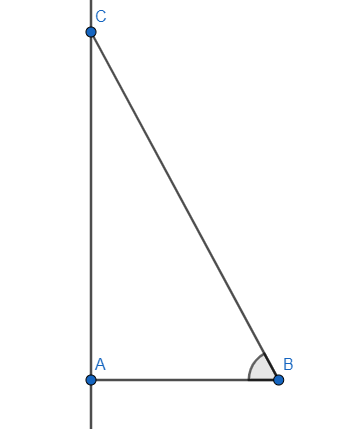
In this case we take $AB=1$ and keeping the ratio in mind we have $BC=x$ as the ratio has to be $\dfrac{1}{x}$. Now we apply the Pythagoras’ theorem to find the length of AC. $B{{C}^{2}}=A{{B}^{2}}+A{{C}^{2}}$.
So, $A{{C}^{2}}={{x}^{2}}-1$ which gives $AC=\sqrt{{{x}^{2}}-1}$. We took positive value as $\theta$ is an acute angle.
We need to find $\tan \theta$. This ratio gives $\tan \theta =\dfrac{\text{height}}{\text{base}}$. So, $\tan \theta =\dfrac{AC}{AB}=\dfrac{\sqrt{{{x}^{2}}-1}}{1}=\sqrt{{{x}^{2}}-1}$.
Therefore, the correct option is (B).

Note:
We can also apply the trigonometric image form to get the value of $\tan \theta$.
The value $\cos \theta =\dfrac{1}{x}$ gives that $\sec \theta =x$. We know $\sec \theta =\sqrt{1+{{\tan }^{2}}\theta }$.
Putting the values, we get $\tan \theta =\sqrt{{{\sec }^{2}}\theta -1}=\sqrt{{{x}^{2}}-1}$.