Question

If $\theta$ be the angle between two tangents which are drawn to the circles ${{\text{x}}^2}{\text{ + }}{{\text{y}}^2}{\text{ - 6}}\sqrt 3 {\text{x - 6y + 27 = 0}}$ from the origin. Then $2\sqrt 3 {\text{tan}}\theta$ equals to
a. 6
b. 3
c. 2
d. 1

Answer 1

Hint: To solve this question we will use the formula to find the angle between two straight line which is $\tan \theta {\text{ = }}\left| {\dfrac{{{{\text{m}}_1}{\text{ - }}{{\text{m}}_2}}}{{1{\text{ + }}{{\text{m}}_1}{{\text{m}}_2}}}} \right|$. We will first find the equation of tangents by using the formula ${\text{(y - }}{{\text{y}}_1}){\text{ = }}\dfrac{{{{\text{y}}_2}{\text{ - }}{{\text{y}}_1}}}{{{{\text{x}}_2}{\text{ - }}{{\text{x}}_1}}}({\text{x - }}{{\text{x}}_1})$. After it, we will find the angle between two tangents by the above formula.

Complete step-by-step answer:
Now, we will draw a figure according to the question. The equation of circle is ${{\text{x}}^2}{\text{ + }}{{\text{y}}^2}{\text{ - 6}}\sqrt 3 {\text{x - 6y + 27 = 0}}$. The centre of the circle is C ($3\sqrt 3$, 3) and radius is 3 units. Let OA and OB are two tangents drawn from origin to the circle. Therefore, the figure is

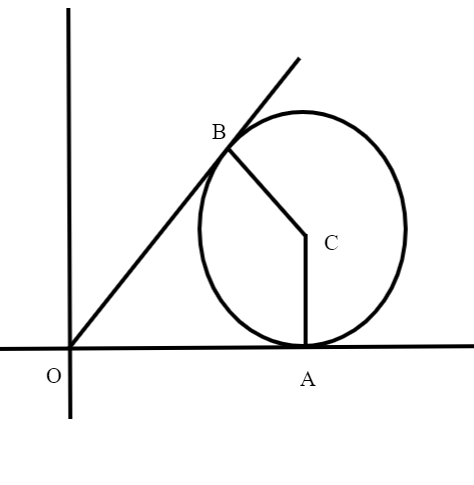
Now, the coordinates of centre C are ($3\sqrt 3$, 3). Let a point B (h, k) be the point of contact. Also, point B lies on the circle. So, it also satisfies the equation of circle. So, we get
${{\text{h}}^2}{\text{ + }}{{\text{k}}^2}{\text{ - 6}}\sqrt 3 {\text{h - 6k + 27 = 0}}$ … (1)
Also, by distance formula, ${\text{d = }}\sqrt {{{{\text{(}}{{\text{x}}_2}{\text{ - }}{{\text{x}}_1})}^2}{\text{ + (}}{{\text{y}}_2}{\text{ - }}{{\text{y}}_1}{)^2}}$ we get
OB = $\sqrt {{{{\text{(h - 0}})}^2}{\text{ + (k - 0}}{)^2}}$ = $\sqrt {{{\text{h}}^2}{\text{ + }}{{\text{k}}^2}}$
Also, the length of tangents from an external point are equal to each other. So, OA = OB.
Now, coordinates of A are ($3\sqrt 3$, 0). So, OA = $3\sqrt 3$
Therefore, from the above property, we get OB = $3\sqrt 3$
$\sqrt {{{\text{h}}^2}{\text{ + }}{{\text{k}}^2}}$ = $3\sqrt 3$
Squaring both sides, we get
${{\text{h}}^2}{\text{ + }}{{\text{k}}^2}{\text{ = 27}}$ … (2)
Therefore, from equation (1), we get
${\text{27 - 6}}\sqrt 3 {\text{h - 6k + 27 = 0}}$
On simplifying the above expression, we get
$\sqrt 3 {\text{h + k = 9}}$
${\text{k = 9 - }}\sqrt 3 {\text{h}}$ … (3)
Putting this value in equation (2), we get
${{\text{h}}^2}{\text{ + (9 - }}\sqrt 3 {\text{h}}{{\text{)}}^2}{\text{ = 27}}$
${{\text{h}}^2}{\text{ + 81 + 3}}{{\text{h}}^2}{\text{ - 18}}\sqrt 3 {\text{h = 27}}$
${\text{4}}{{\text{h}}^2}{\text{ - 18}}\sqrt 3 {\text{h + 54 = 0}}$
On solving, we get
h = $3\sqrt 3$ , $\dfrac{{3\sqrt 3 }}{2}$
so, we get k = 0, $\dfrac{9}{2}$
So, we get A ($3\sqrt 3$, 0) and B ($\dfrac{{3\sqrt 3 }}{2}$, $\dfrac{9}{2}$).
Now, the equation of tangent OA is x = $3\sqrt 3$. So, the slope is 0.
Now, slope of tangent OB = $\dfrac{{\dfrac{9}{2}{\text{ - 0}}}}{{\dfrac{{3\sqrt 3 }}{2}{\text{ - 0}}}}$ = $\sqrt 3$
Now, angle between two tangents = $\tan \theta {\text{ = }}\left| {\dfrac{{{{\text{m}}_1}{\text{ - }}{{\text{m}}_2}}}{{1{\text{ + }}{{\text{m}}_1}{{\text{m}}_2}}}} \right|$, where ${{\text{m}}_1}{\text{ = }}\sqrt 3$ and ${{\text{m}}_2}{\text{ = 0}}$.
$\tan \theta {\text{ = }}\left| {\dfrac{{\sqrt 3 {\text{ - 0}}}}{{1{\text{ - }}\sqrt 3 {\text{(0)}}}}} \right|$ = $\sqrt 3$
Now, $2\sqrt 3 {\text{tan}}\theta$ = $2(\sqrt 3 )(\sqrt 3 )$ = 6
So, option (a) is correct.

Note: When we come up with such types of questions, we will use the formula $\tan \theta {\text{ = }}\left| {\dfrac{{{{\text{m}}_1}{\text{ - }}{{\text{m}}_2}}}{{1{\text{ + }}{{\text{m}}_1}{{\text{m}}_2}}}} \right|$ to find the angle between two lines. We will follow a few steps to solve the given problem. We will first let a point which satisfies the equation of circle. Then, we will apply the property of tangents to find the value of the point. We will also use the distance formula to find the value of the point. The value of point gives the coordinates of two tangents drawn from an external point. After finding the point, we will find the slopes of each tangent and apply the above formula to find the required answer.