Question

If there is an increase in a series at constant rate, the graph will be a _______.
${\text{A)}}$ Convex curve
${\text{B)}}$ Concave curve
${\text{C)}}$ A straight line from left top to right bottom
${\text{D)}}$ A straight line from left bottom to right top

Answer 1

To find the answer without any doubt, we have to assume and consider a series first, and then increase the series at a constant rate i.e., with the same amount or number.
After that, we will represent in a graph and also we will be able to see the cures and lines clearly
Finally we get the required answer.

Complete step-by-step solution:
Let us assume a simple series distribution which is increasing at constant rate:

${\text{x}}$	$1$	$2$	$3$	$4$	$5$	$6$
${\text{y}}$	$5$	$10$	$15$	$20$	$25$	$30$

Here, every number is increasing by $5$ (thus at constant rate)
Now, representing this table in the graph, we get:

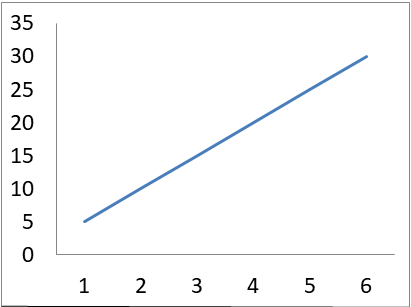
As we can see, the change in the graph is a straight line from left bottom to right top.

Hence we can conclude the correct option is (D) A straight line from left bottom to right top.

Note: In this question we have an alternative logical answer as follows:
Basically a series consists of a sequence with some common operations in it and almost in every case, the number will be increasing in certain rate and sometimes it will be in a decreasing rate too.
Considering in that way, when the numbers are increasing at a constant rate, the difference between the points will be the same and the points in the graph will also increase in a constant rate as the difference is the same, thus we will get a straight line from left bottom to right top.
In case, if the series is decreasing at a constant rate, the graph will be a straight line from left top to right bottom.