Question

If there exist a chord a parabola y = ax² + bx, a, b ∈R,a≠0,b≠0, such that the end points of the chord are (p, q) and (q, p) for some p, q ∈Rand p≠q then the least possible positive integral value of b is

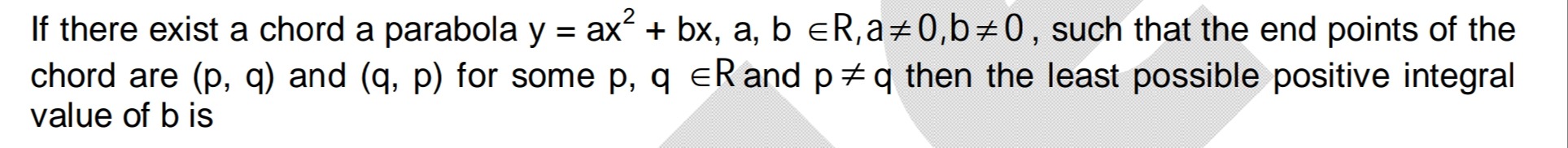
• A. 1
• B. 2
• C. 3
• D. 4

Answer 1

Answer: (D)

4

Answer 2

Let the equation of the parabola be $y = ax^2 + bx$, where $a, b \in \mathbb{R}$, $a \neq 0$, $b \neq 0$. Let the end points of the chord be $(p, q)$ and $(q, p)$, where $p, q \in \mathbb{R}$ and $p \neq q$. Since these points lie on the parabola, they must satisfy the equation of the parabola.

For point $(p, q)$: $q = ap^2 + bp \quad (1)$ For point $(q, p)$: $p = aq^2 + bq \quad (2)$

Subtracting equation (2) from equation (1): $q - p = (ap^2 + bp) - (aq^2 + bq)$ $q - p = a(p^2 - q^2) + b(p - q)$ $q - p = a(p - q)(p + q) + b(p - q)$

Since $p \neq q$, we know that $p - q \neq 0$. We can divide both sides by $(p - q)$: $\frac{q - p}{p - q} = a(p + q) + b$ $-1 = a(p + q) + b$ $a(p + q) = -1 - b$ Since $a \neq 0$, we can write $p + q = \frac{-1 - b}{a}$.

Adding equation (1) and equation (2): $q + p = (ap^2 + bp) + (aq^2 + bq)$ $p + q = a(p^2 + q^2) + b(p + q)$ Let $S = p + q$ and $P = pq$. The equation becomes: $S = a(S^2 - 2P) + bS$ $S - bS = a(S^2 - 2P)$ $S(1 - b) = a(S^2 - 2P)$

Substitute $S = \frac{-1 - b}{a}$: $\frac{-1 - b}{a}(1 - b) = a\left(\left(\frac{-1 - b}{a}\right)^2 - 2P\right)$ $\frac{-(1 + b)(1 - b)}{a} = a\left(\frac{(1 + b)^2}{a^2} - 2P\right)$ $\frac{b^2 - 1}{a} = a\left(\frac{(1 + b)^2 - 2a^2 P}{a^2}\right)$ $\frac{b^2 - 1}{a} = \frac{(1 + b)^2 - 2a^2 P}{a}$ Multiply by $a$ (since $a \neq 0$): $b^2 - 1 = (1 + b)^2 - 2a^2 P$ $b^2 - 1 = 1 + 2b + b^2 - 2a^2 P$ $-1 = 1 + 2b - 2a^2 P$ $2a^2 P = 1 + 1 + 2b$ $2a^2 P = 2 + 2b$ $a^2 P = 1 + b$ Since $a \neq 0$, $a^2 > 0$, so $P = pq = \frac{1 + b}{a^2}$.

Now we have the sum $p+q = \frac{-1-b}{a}$ and the product $pq = \frac{1+b}{a^2}$. $p$ and $q$ are the roots of the quadratic equation $x^2 - (p+q)x + pq = 0$. $x^2 - \left(\frac{-1-b}{a}\right)x + \frac{1+b}{a^2} = 0$ $x^2 + \frac{1+b}{a}x + \frac{1+b}{a^2} = 0$ Multiplying by $a^2$ (since $a \neq 0$): $a^2 x^2 + a(1+b)x + (1+b) = 0$

For $p$ and $q$ to be real and distinct roots (since $p \neq q$), the discriminant of this quadratic equation must be positive. The discriminant $D = (a(1+b))^2 - 4(a^2)(1+b)$. $D = a^2 (1+b)^2 - 4a^2 (1+b)$ The condition $D > 0$ is: $a^2 (1+b)^2 - 4a^2 (1+b) > 0$ Since $a \neq 0$, $a^2 > 0$. We can divide by $a^2$: $(1+b)^2 - 4(1+b) > 0$ Let $X = 1+b$. The inequality becomes: $X^2 - 4X > 0$ $X(X - 4) > 0$

This inequality holds when $X < 0$ or $X > 4$. Case 1: $X < 0$ $1 + b < 0$ $b < -1$

Case 2: $X > 4$ $1 + b > 4$ $b > 3$

So, the possible values for $b$ are $b < -1$ or $b > 3$. We are given that $b \in \mathbb{R}$ and $b \neq 0$. The condition $b < -1$ or $b > 3$ automatically satisfies $b \neq 0$.

We are looking for the least possible positive integral value of $b$. The set of possible values for $b$ is $(-\infty, -1) \cup (3, \infty)$. We are looking for positive integers in this set. The integers in $(-\infty, -1)$ are $\dots, -3, -2$. None of these are positive. The integers in $(3, \infty)$ are $4, 5, 6, \dots$. These are all positive integers. The least positive integral value in this set is 4.

For $b=4$, the condition $b > 3$ is satisfied, so there exist distinct real numbers $p, q$ which are the roots of $a^2 x^2 + a(1+4)x + (1+4) = 0$, i.e., $a^2 x^2 + 5ax + 5 = 0$. For any $a \neq 0$, the discriminant $5a^2 > 0$, so distinct real roots exist. These roots $p, q$ satisfy $p+q = -5/a$ and $pq = 5/a^2$. From our derivation, if $p, q$ are distinct real roots of this equation, then $(p, q)$ and $(q, p)$ lie on $y = ax^2 + bx$ with $b=4$.

The least possible positive integral value of $b$ is 4.