Solveeit Logo
Login

Question

Question: If , then find the value of : A.\[\dfrac{{\sqrt {1 - {a^2} + a} }}{{\sqrt {1 - {a^2}} }}\] B.\[\...

If , then find the value of :
A.1−a2+a1−a2\dfrac{{\sqrt {1 - {a^2} + a} }}{{\sqrt {1 - {a^2}} }}
B.1−a2+11−a2\dfrac{{\sqrt {1 - {a^2} + 1} }}{{\sqrt {1 - {a^2}} }}
C.a(1−a2 + 1)1−a2\dfrac{{a(\sqrt {1 - {a^2}} \, + \,1)}}{{\sqrt {1 - {a^2}} }}
D.1+1−a21−a2\dfrac{{1 + \sqrt {1 - {a^2}} }}{{\sqrt {1 - {a^2}} }}

Explanation

Solution

First, we have to define what the terms we need to solve the problem are.Each degree is then further divided into 6060 minutes denoted by ‘, for example
10∘6′{10^ \circ }6'
Each minute is then further divided into 6060 seconds denoted by “, for example
This can be pronounced as “Ten degrees six minutes thirty-two seconds”
Here we are given
To find the required answer, we need to find cos and tan in terms of a using

Formula to be used:

sin⁡(90∘−θ)=cos⁡θ\sin ({90^ \circ } - \theta ) = \cos \theta
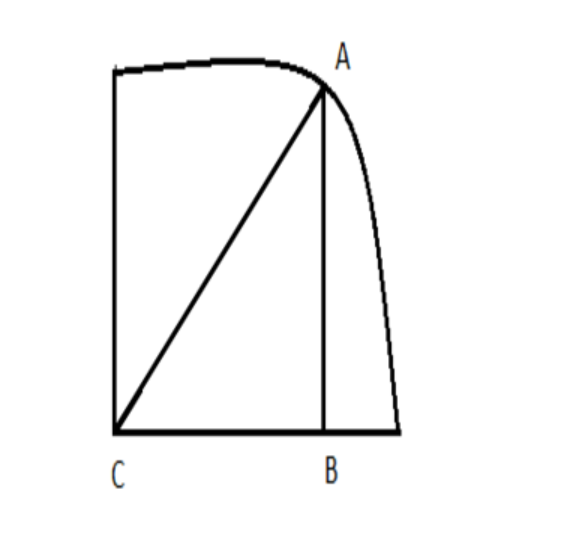
According to Pythagoras theorem
AB2+BC2=AC2A{B^2} + B{C^2} = A{C^2}
AC=AC = hypotenuse
AB=AB = perpendicular
BC=BC = base
In trigonometry,
Let ∠ACB=θ\angle ACB = \theta
sin⁡2θ+cos⁡2θ=1{\sin ^2}\theta + {\cos ^2}\theta = 1
sin⁡θ=PerpendicularHypotenuse\sin \theta = \dfrac{{Perpendicular}}{{Hypotenuse}}
cos⁡θ=BaseHypotenuse\cos \theta = \dfrac{{Base}}{{Hypotenuse}}
tan⁡θ=PerpendicularBase\tan \theta = \dfrac{{Perpendicular}}{{Base}}
tan⁡θ=sin⁡θcos⁡θ\tan \theta = \dfrac{{\sin \theta }}{{\cos \theta }}

Complete answer:
It is given that
=PerpendicularHypotenuse\dfrac{{Perpendicular}}{{Hypotenuse}}
Since,
AC=AC = hypotenuse
AB=AB = perpendicular
BC=BC = base
And,
AB2+BC2=AC2A{B^2} + B{C^2} = A{C^2}
We can find the value of the base with this equation and place all the values:
BC2=AC2−AB2B{C^2} = A{C^2} - A{B^2}
BC=AC2−AB2BC = \sqrt {A{C^2} - A{B^2}}
BC=1−a2BC = \sqrt {1 - {a^2}}
So the base is 1−a2\sqrt {1 - {a^2}}
Now we can find cos value for that same angle θ\theta , by applying the Pythagoras theorem for trigonometric identities
Since we know, the value of both sin and cos
tan⁡θ=sin⁡θcos⁡θ\tan \theta = \dfrac{{\sin \theta }}{{\cos \theta }}
So, to find the value of tan⁡θ\tan \theta
And also,
sin⁡(90∘−θ)=cos⁡θ\sin ({90^ \circ } - \theta ) = \cos \theta
Make sure that the value of minute and second do not exceed 6060.
Now we know the value of and
So adding both we get

Hence, the correct option is (C) a(1−a2 + 1)1−a2\dfrac{{a(\sqrt {1 - {a^2}} \, + \,1)}}{{\sqrt {1 - {a^2}} }}

Note:
Using the given , we need to apply the Pythagoras theorem. Applying the theorem, we are able to find the value of the base, the perpendicular, and the hypotenuse.
The concept of angle: A circle is divided into 360360 equal parts. It is known as the degree where there is a sign of negative sign and a degree greater than 360360 in degree used in trigonometric terms, it is one of the measurement units in angle.