Question

If the work done by a body on application of a constant force is directly proportional to the distance travelled by the body, express this in the form of an equation in two variables and draw the graph of the same by taking the constant force as 5 units.
Also read from the graph the work done when the distance travelled by the body is
(i) 2 units (ii) 5 units

Answer 1

ince, it is given that work done is directly proportional to distance travelled by body
$\Rightarrow y \propto x$
So, we can write this equation as:
$y = kx$ , here k is a constant force.
It is given that constant force = 5 units
i.e. k = 5.
So, our equation becomes $y = 5x$
Use this equation to plot graphs, for plotting graphs first put the value of x = 0 in the above linear equation, from this you will get the corresponding value of y = 0. This is the point of origin $O\left( {0,0} \right)$.
Similarly, on putting x = 1 you will get y = 5. This is point $A\left( {1,5} \right)$.
Draw a line passing through point O and A, this will be the line for the given equation.

Complete step-by-step Solution:
Let the distance travelled by the body be x
And let the work done by the body be y
It is given that work done is directly proportional to distance travelled by body:
$\Rightarrow y \propto x$
So, we can write the above equation as:
$y = kx$ , where k is a constant.
Here, k is the constant force applied on the body.
It is given that the value of constant force = 5 units
i.e. k = 5.
So, our equation becomes $y = 5x$ -------------->[1]
We need to draw graph:
In eq(i) $y = 5x$
Putting x = 0, we get:
$y = 5(0) = 0$
So, (0,0) is a solution of the equation
Now, putting x = 1 we get:
$y = 5\left( 1 \right) = 5$
So, (1,5) is a solution of the equation.

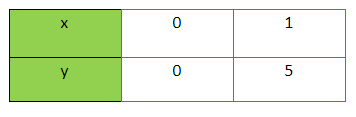
Hence, the line $y = 5x$ passes through points $A\left( {0,0} \right){\text{ and }}B\left( {1,5} \right)$.
Plotting points A and B and drawing a line passing through them we get the graph of function $y = 5x$
Where y-axis represents total work done and x-axis represents displacement of the body.

Calculating work done by graph when the distance travelled by the body is:
(i) 2 units
Expression for work done is:
$y = 5x$
Here, y is work done and x is distance travelled.
Given, distance travelled is 2 units i.e. x = 2
Putting x = 2 in expression for work we get:
$y = 5\left( 2 \right) = 10$
Therefore, work done is 10 units.
Same result can also be seen by graph:

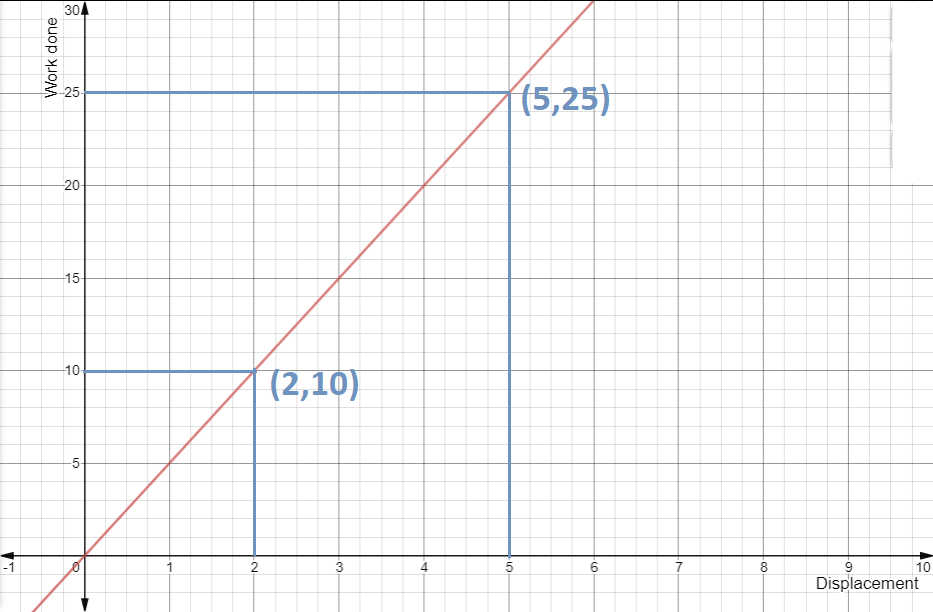
(ii) distance travelled by the body is 5 units
Similarly, putting x = 5 in expression for work we get:
$y = 5\left( 5 \right) = 25$
Therefore, work done in this case is 25 units.

Note: The graph of linear equations of the form $y = mx$ always passes through origin with some angle with the horizontal I.e. x-axis.