Question
Question: If the wavelength of limiting line of Lyman series for $He^+$ ion is $x$ Å, then what will be the wa...
If the wavelength of limiting line of Lyman series for He+ ion is x Å, then what will be the wavelength of limiting line of Balmer Series for Li+2 ion.
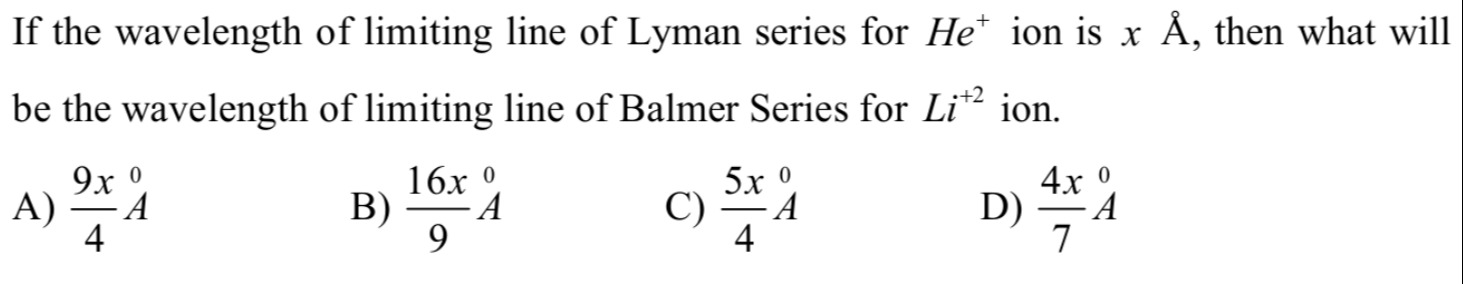
49xA
916xA
45xA
74xA
916xA
Solution
The problem involves calculating wavelengths of spectral lines using the Rydberg formula for hydrogen-like atoms.
Key Concept:
The Rydberg formula for the wavelength (λ) of a spectral line in a hydrogen-like atom is given by:
λ1=RZ2(n121−n221)where:
- R is the Rydberg constant.
- Z is the atomic number of the atom/ion.
- n1 is the principal quantum number of the lower energy level.
- n2 is the principal quantum number of the higher energy level.
For a "limiting line" in any series, the electron transition occurs from n2=∞ to the specific n1 for that series.
Step-by-step Derivations:
1. For He+ ion (Lyman series, limiting line):
- Ion: He+
- Atomic Number (Z): For Helium, Z=2.
- Series: Lyman series, which means the electron transitions to the n1=1 energy level.
- Line: Limiting line, so the electron originates from n2=∞.
- Given Wavelength: λ=x Å.
Applying the Rydberg formula:
x1=R(2)2(121−∞21) x1=R⋅4(11−0) x1=4RFrom this, we can express the Rydberg constant R in terms of x:
R=4x1(Equation 1)2. For Li+2 ion (Balmer series, limiting line):
- Ion: Li+2
- Atomic Number (Z): For Lithium, Z=3.
- Series: Balmer series, which means the electron transitions to the n1=2 energy level.
- Line: Limiting line, so the electron originates from n2=∞.
- Required Wavelength: Let this be λ′.
Applying the Rydberg formula:
λ′1=R(3)2(221−∞21) λ′1=R⋅9(41−0) λ′1=49R(Equation 2)3. Substitute Equation 1 into Equation 2:
Now, substitute the value of R from Equation 1 into Equation 2:
λ′1=49(4x1) λ′1=16x9Solving for λ′:
λ′=916xThus, the wavelength of the limiting line of the Balmer series for the Li+2 ion is 916x Å.
