Question

If the volume of a tetrahedron formed by coterminous edges $\vec a$, $\vec b$, $\vec c$ is 2, then what is the volume of the parallelepiped formed by the coterminous edges $\vec a \times \vec b$, $\vec b \times \vec c$, $\vec c \times \vec a$?
A.72
B.144
C.36
D.108

Answer 1

The volume of a tetrahedron formed by coterminous edges $\vec a$, $\vec b$, $\vec c$ is given by \dfrac{1}{6}\left[ {\begin{array}{*{20}{c}} {\vec a}&{\vec b}&{\vec c} \end{array}} \right]. The volume of a parallelepiped formed by the coterminous edges $\vec a \times \vec b$, $\vec b \times \vec c$, $\vec c \times \vec a$ is given by \left[ {\begin{array}{*{20}{c}} {\vec a \times \vec b}&{\vec b \times \vec c}&{\vec c \times \vec a} \end{array}} \right].

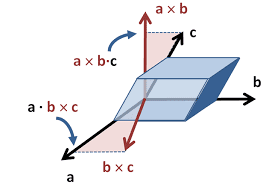
Complete step-by-step answer:
The volume of a parallelepiped with coterminous edges $\vec a$, $\vec b$, $\vec c$ is given by the formula \left[ {\begin{array}{*{20}{c}} {\vec a}&{\vec b}&{\vec c} \end{array}} \right], which is the scalar triple product of the vectors which form the edges of the parallelepiped. The volume of a tetrahedron is one-sixth the volume of parallelepiped, therefore its volume is given by \dfrac{1}{6}\left[ {\begin{array}{*{20}{c}} {\vec a}&{\vec b}&{\vec c} \end{array}} \right].
Since we do not know the vectors, we will have to find out the value of \left[ {\begin{array}{*{20}{c}} {\vec a}&{\vec b}&{\vec c} \end{array}} \right] by using the volume of the tetrahedron given.

{\vec a}&{\vec b}&{\vec c} \end{array}} \right] = 2 \Rightarrow \left[ {\begin{array}{*{20}{c}} {\vec a}&{\vec b}&{\vec c} \end{array}} \right] = 12$$ …equation (1) We have obtained the value of the scalar triple product of the vectors $\vec a$, $\vec b$, $$\vec c$$. Now we can find out the volume of the parallelepiped formed by the coterminous edges $\vec a \times \vec b$, $\vec b \times \vec c$, $\vec c \times \vec a$. Volume of parallelepiped = $\left[ {\begin{array}{*{20}{c}} {\vec a \times \vec b}&{\vec b \times \vec c}&{\vec c \times \vec a} \end{array}} \right] = {\left[ {\begin{array}{*{20}{c}} {\vec a}&{\vec b}&{\vec c} \end{array}} \right]^2}$ …equation (2) We substitute the value obtained in equation (1) in equation (2) and obtain, Volume of parallelepiped = ${\left[ {\begin{array}{*{20}{c}} {\vec a}&{\vec b}&{\vec c} \end{array}} \right]^2} = {\left( {12} \right)^2} = 144$ Hence, the volume of the parallelepiped formed by the coterminous edges $\vec a \times \vec b$, $\vec b \times \vec c$, $\vec c \times \vec a$ is 144. **Therefore, the correct option for the given question is option B.** **Note:** The proof of $\left[ {\begin{array}{*{20}{c}} {\vec a \times \vec b}&{\vec b \times \vec c}&{\vec c \times \vec a} \end{array}} \right] = {\left[ {\begin{array}{*{20}{c}} {\vec a}&{\vec b}&{\vec c} \end{array}} \right]^2}$ is given below. $\left[ {\begin{array}{*{20}{c}} {\vec a \times \vec b}&{\vec b \times \vec c}&{\vec c \times \vec a} \end{array}} \right] = \left( {\vec a \times \vec b} \right) \cdot \left[ {\left( {\vec b \times \vec c} \right) \times \left( {\vec c \times \vec a} \right)} \right]$ Expanding the quadruple vector product on the right hand side of the equation, we obtain, $\left[ {\begin{array}{*{20}{c}} {\vec a \times \vec b}&{\vec b \times \vec c}&{\vec c \times \vec a} \end{array}} \right] = \left( {\vec a \times \vec b} \right) \cdot \left[ {\left( {\left( {\vec b \times \vec c} \right) \cdot \vec a} \right) \cdot \vec c - \left( {\left( {\vec b \times \vec c} \right) \cdot \vec c} \right) \cdot \vec a} \right]$ Upon simplifying, we obtain, $\left[ {\begin{array}{*{20}{c}} {\vec a \times \vec b}&{\vec b \times \vec c}&{\vec c \times \vec a} \end{array}} \right] = \left( {\vec a \times \vec b} \right) \cdot \left[ {\left[ {\begin{array}{*{20}{c}} {\vec b}&{\vec c}&{\vec a} \end{array}} \right]\vec c - \left[ {\begin{array}{*{20}{c}} {\vec b}&{\vec c}&{\vec c} \end{array}} \right]\vec a} \right]$ But, $$\left[ {\begin{array}{*{20}{c}} {\vec b}&{\vec c}&{\vec c} \end{array}} \right]$$ = 0 and $$\left[ {\begin{array}{*{20}{c}} {\vec b}&{\vec c}&{\vec a} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\vec a}&{\vec b}&{\vec c} \end{array}} \right]$$ $ \Rightarrow \left[ {\begin{array}{*{20}{c}} {\vec a \times \vec b}&{\vec b \times \vec c}&{\vec c \times \vec a} \end{array}} \right] = \left( {\vec a \times \vec b} \right) \cdot \left[ {\left[ {\begin{array}{*{20}{c}} {\vec a}&{\vec b}&{\vec c} \end{array}} \right]\vec c - 0} \right]$ $ \Rightarrow \left[ {\begin{array}{*{20}{c}} {\vec a \times \vec b}&{\vec b \times \vec c}&{\vec c \times \vec a} \end{array}} \right] = \left( {\vec a \times \vec b} \right) \cdot \vec c\left[ {\begin{array}{*{20}{c}} {\vec a}&{\vec b}&{\vec c} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\vec a}&{\vec b}&{\vec c} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\vec a}&{\vec b}&{\vec c} \end{array}} \right] = {\left[ {\begin{array}{*{20}{c}} {\vec a}&{\vec b}&{\vec c} \end{array}} \right]^2}$ Hence, proved.