Solveeit Logo
Login

Question

Question: If the vertices of a triangle are (1,-3), (4,p) and (-9,7) and its area is 15 sq. units, then find t...

If the vertices of a triangle are (1,-3), (4,p) and (-9,7) and its area is 15 sq. units, then find the value (s) of p.

Explanation

Solution

The formula ar(ΔABC)=12[x1(y2−y3)+x2(y3−y1)+x3(y1−y2)]ar\left( \Delta ABC \right)=\dfrac{1}{2}\left[ {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right] for any three coordinates A(x1,y1),B(x2,y2),C(x3,y3)A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right),C\left( {{x}_{3}},{{y}_{3}} \right) of a triangle is used to find the value of p after substituting all the given values in the above-mentioned equation.

Complete step by step answer:
Let us consider a triangle ABC with the coordinates A (1, -3), B (4, p) and C (-9,7).

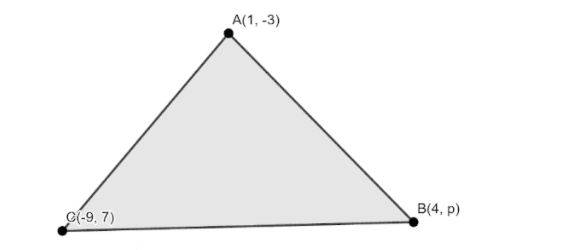
We know, the area of a triangle ABC with the three coordinates A(x1,y1),B(x2,y2),C(x3,y3)A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right),C\left( {{x}_{3}},{{y}_{3}} \right) is given by the numerical value of the expression
ar(ΔABC)=12[x1(y2−y3)+x2(y3−y1)+x3(y1−y2)]…(i)ar\left( \Delta ABC \right)=\dfrac{1}{2}\left[ {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right]\ldots \left( i \right)
Here,
(x1,y1)=(1,−3) (x2,y2)=(4,p) (x3,y3)=(−9,7) ar(ΔABC)=15 \begin{aligned} & \left( {{x}_{1}},{{y}_{1}} \right)=\left( 1,-3 \right) \\\ & \left( {{x}_{2}},{{y}_{2}} \right)=\left( 4,p \right) \\\ & \left( {{x}_{3}},{{y}_{3}} \right)=\left( -9,7 \right) \\\ & ar\left( \Delta ABC \right)=15 \\\ \end{aligned}
Substituting these values in equation (i), we get
15=12[1(p−7)+4(7−(−3))+−9(−3−p)]15=\dfrac{1}{2}\left[ 1\left( p-7 \right)+4\left( 7-(-3) \right)+-9\left( -3-p \right) \right]
Solving this, we get
 12[(p−7)+4(7+3)−9(−3−p)]=15 ⇒p−7+40+27+9p=30 ⇒p+9p=30−27+7−40 ⇒10p=−30 ⇒p=−3 \begin{aligned} & \text{ }\dfrac{1}{2}\left[ \left( p-7 \right)+4\left( 7+3 \right)-9\left( -3-p \right) \right]=15 \\\ & \Rightarrow p-7+40+27+9p=30 \\\ & \Rightarrow p+9p=30-27+7-40 \\\ & \Rightarrow 10p=-30 \\\ & \Rightarrow p=-3 \\\ \end{aligned}

Hence, the value of p is -3.

Note: We should use this formula and do the calculations with utmost care, because a single error will change the answer. Always double-check the formula and calculations after solving. We should keep in mind that area is a measure, that is, it cannot be negative. If the area of a triangle comes out zero, then it means that the three points are collinear points. The best way to remember this formula is to remember the cycle of 1, 2, 3.

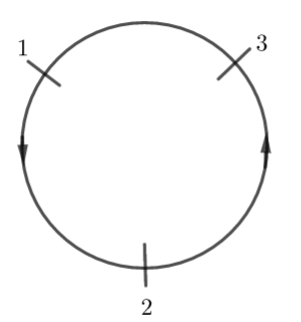
The cycle goes as 1, 2, 3 which means the first expression is x1(y2−y3){{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right).
Then the cycle moves to 2, 3, 1 which means the second expression is x2(y3−y1){{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right). Then the cycle moves further as 3, 2, 1 which means the third expression is x3(y1−y2){{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right). Once we remember these three expressions correctly, then the rest of the formula can be easily remembered.