Question

If the vertices of a parallelogram are respectively $(0,0)$ , $(1,0)$, $(2,2)$ and $(1,2)$ , then the angle between diagonals is
1. $\dfrac{\pi }{3}$
2. $\dfrac{\pi }{2}$
3. $\dfrac{3\pi }{2}$
4. $\dfrac{\pi }{4}$

Answer 1

In this question firstly assume the angle between diagonals equals to $\theta$ then assume the slope of lines $BD,AC$ as ${{m}_{2}},{{m}_{1}}$ respectively then find out the value of these slope and then apply the formula for slope of angles between two lines then check which option is correct among these given options.

Complete step by step answer:
Parallelepiped is a three-dimensional shape with parallelogram-shaped faces. The area of a parallelogram is determined by its base, one of its parallel sides and height; the height measured from top to bottom. The length of a parallelogram's four sides determines its perimeter. It's a four-sided polygon sometimes known as a quadrilateral with two parallel sides that are the same length. A parallelogram's interior opposing angles are also equal in size. The sum of a parallelogram's neighbouring angles is $180$ degrees. A quadrilateral with two pairs of parallel sides is known as a parallelogram. The lengths of the opposite sides of a parallelogram are equal, as are the measures of the opposite angles. A parallelogram is a quadrilateral with both pairs of opposite sides parallel.
Now according to the question:

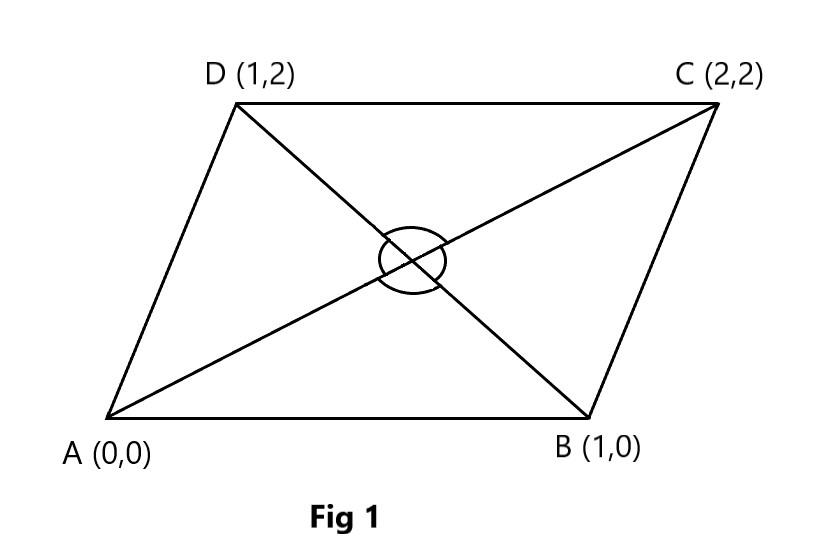
In the figure $(1)$ we have given four sides of parallelogram that is $A,B,C,D$
And $BD,AC$ are the diagonals of parallelogram.
Let the angle between the diagonals is $\theta$
Let the slope of $BD={{m}_{1}}$ and the slope of $AC={{m}_{2}}$
As we know that to find the slope we can apply the formula:
$\Rightarrow slope=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$
Now we will find out the slope of $BD$ hence:
$\Rightarrow {{m}_{1}}=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$
Where ${{x}_{1}}=1,{{y}_{1}}=0,{{x}_{2}}=1,{{y}_{2}}=2$ , now putting these values to get the slope:
$\Rightarrow {{m}_{1}}=\dfrac{2-0}{1-1}$
$\Rightarrow {{m}_{1}}=\dfrac{2}{0}$
$\Rightarrow {{m}_{1}}=\infty$
Now we will find out the slope for $AC$ hence:
$\Rightarrow {{m}_{2}}=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$
Where ${{x}_{1}}=0,{{y}_{1}}=0,{{x}_{2}}=2,{{y}_{2}}=0$ , now putting these values to get the slope:
$\Rightarrow {{m}_{2}}=\dfrac{2-0}{2-0}$
$\Rightarrow {{m}_{2}}=\dfrac{2}{2}$
$\Rightarrow {{m}_{2}}=1$
We know that slope of angle between two lines can be calculated by:
$\Rightarrow \tan \theta =\left| \dfrac{{{m}_{2}}-{{m}_{1}}}{1+{{m}_{1}}{{m}_{2}}} \right|$
Where ${{m}_{1}}=\infty$ and ${{m}_{2}}=1$ , putting these values to get the value of angle we will get:
$\Rightarrow \tan \theta =\left| \dfrac{1-\infty }{1+1\times \infty } \right|$
$\Rightarrow \tan \theta =\infty$
$\Rightarrow \theta ={{\tan }^{-1}}\infty$
As we know that ${{\tan }^{-1}}\infty =\dfrac{\pi }{2}$ hence:
$\Rightarrow \theta =\dfrac{\pi }{2}$

So, the correct answer is “Option 2”.

Note:
A good fact about a parallelogram is that it has two pairs of parallel sides that never meet, as well as four edges, and the opposite sides and opposite angles of a parallelogram are congruent. The word parallelogram derives from the Greek word parallelogramma.