Question

If the vectors $\overrightarrow a = 3\widehat i + \widehat j - 2\widehat k,\overrightarrow b = - \widehat i + 3\widehat j + 4\widehat k$ and $\overrightarrow c = 4\widehat i - 2\widehat j - 6\widehat k$ constitute the sides of a $\Delta ABC,$ then the length of the median bisecting the vector $\overrightarrow c$ is
A. $\sqrt 2$
B. $\sqrt {14}$
C. $\sqrt {74}$
D. $\sqrt 6$

Answer 1

Hint : Length of the median is the vertex to the midpoint of the opposite side. Here we will first calculate the magnitude of the given vectors and then substitute the values of the magnitude of the vectors in the formula $L = \dfrac{1}{2}\sqrt {2({a^2} + {b^2}) - {c^2}}$ and simplify for the resultant answer.

Complete step-by-step answer :
Take vectors and write respective sides of the given vectors.
$\overrightarrow a = 3\widehat i + \widehat j - 2\widehat k = \overrightarrow {BC} \\\ \overrightarrow b = - \widehat i + 3\widehat j + 4\widehat k = \overrightarrow {AC} \\\ \overrightarrow c = 4\widehat i - 2\widehat j - 6\widehat k = \overrightarrow {AB} \\\$
Find its magnitude-
For vector $\overrightarrow a = 3\widehat i + \widehat j - 2\widehat k = \overrightarrow {BC}$
$\Rightarrow {\left| {\overrightarrow a } \right|^2} = {3^2} + {1^2} + {2^2}$
Simplify the above equation-
$\Rightarrow {\left| {\overrightarrow a } \right|^2} = 9 + 1 + 4 \\\ \Rightarrow {\left| {\overrightarrow a } \right|^2} = 14\;{\text{ }}....{\text{ (i)}} \\\$
For vector, $\overrightarrow b = - \widehat i + 3\widehat j + 4\widehat k = \overrightarrow {AC}$
$\Rightarrow {\left| {\overrightarrow b } \right|^2} = {( - 1)^2} + {3^2} + {4^2}$
Simplify the above equation-
$\Rightarrow {\left| {\overrightarrow b } \right|^2} = 1 + 9 + 16 \\\ \Rightarrow {\left| {\overrightarrow b } \right|^2} = 26\;{\text{ }}....{\text{ (ii)}} \;$
For vector, $\overrightarrow c = 4\widehat i - 2\widehat j - 6\widehat k = \overrightarrow {AB}$
$\Rightarrow {\left| {\overrightarrow c } \right|^2} = {4^2} + {( - 2)^2} + {( - 6)^2}$
Simplify the above equation-
$\Rightarrow {\left| {\overrightarrow c } \right|^2} = 16 + 4 + 36 \\\ \Rightarrow {\left| {\overrightarrow c } \right|^2} = 56\;{\text{ }}....{\text{ (iii)}} \;$

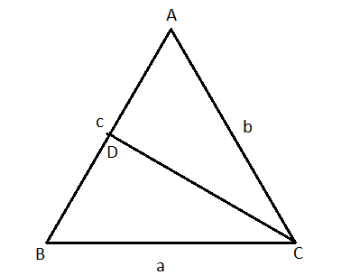
The median of the triangle is the line-segment joining a vertex to the mid-point of the opposite side thus bisecting that opposite side.
The length of the median bisecting the vector C is passing through AC,
$\Rightarrow L = \dfrac{1}{2}\sqrt {2({a^2} + {b^2}) - {c^2}}$
Place values in the above equation using equations (i), (ii) and (iii) –
$\Rightarrow L = \dfrac{1}{2}\sqrt {2(14 + 26) - 56}$
Simplify the above equation –
$\Rightarrow L = \dfrac{1}{2}\sqrt {2(40) - 56} \\\ \Rightarrow L = \dfrac{1}{2}\sqrt {80 - 56} \\\ \Rightarrow L = \dfrac{1}{2}\sqrt {24} \\\$
The above equation can be re-written as –
$\Rightarrow L = \dfrac{1}{2}\sqrt {4 \times 6}$
We know that - $4 = 2 \times 2 = {2^2}$ . place it in the above equation-
$\Rightarrow L = \dfrac{1}{2}\sqrt {{2^2} \times 6}$
Square and square-root cancel each other.
$\Rightarrow L = \dfrac{2}{2}\sqrt 6$
Same terms from the numerator and the denominator cancel each other.
$\Rightarrow L = \sqrt 6$ Units
Hence, from the given multiple choices- the option D is the correct answer.
So, the correct answer is “Option D”.

Note : Remember the general formula for the median of the vectors. Know the difference between the median of the vectors and the median of the numbers. Each triangle has exactly the three medians, one from each vertex, and all the three vertices intersect each other at the point called the Centroid of the triangle.