Question
Question: If the vectors \(\hat{i}-3\hat{j}+2\hat{k},\ -\hat{i}+2\hat{j}\) represents the diagonal of a parall...
If the vectors i^−3j^+2k^, −i^+2j^ represents the diagonal of a parallelogram, then its area will be
(a) 21
(b) 221
(c) 221
(d) 421
Solution
Hint: Area of a parallelogram with two adjacent sides given in form, a and b is
Area of parallelogram = a×b
Use the triangle law of vector addition to get the sides of the parallelogram from the given vectors of the diagonals. Law is given as when two vectors are added and represented as two sides of a triangle in the same order then the third side of the triangle gives the resultant of the other two.
Complete step-by-step answer:
We know that area of parallelogram in terms of the vectors representing their sides can be given as
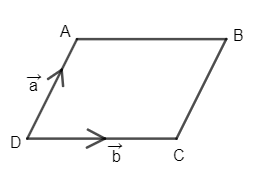
Area of parallelogram ABCD = a×b
It means the area of a parallelogram is the magnitude of the cross-product of any two adjacent sides in vector form.
Here, from the given problem, we have two vectors which are representing the diagonals of parallelogram. These are given as (i^−3j^+2k^) and ( −i^+2j^) . So, we can draw diagram as
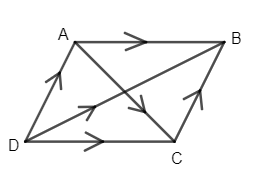
So, let we have parallelogram, whose diagonals are given as
AC = i^−3j^+2k^
DB = −i^+2j^
Now, we know the triangle property of addition of the vectors that when two sides of a triangle are represented by two sides of a triangle in magnitude and direction taken in the same order than the third side of that triangle represents the magnitude and direction resultant of both the vectors. So, we can get from the below triangle as
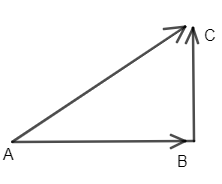
AC= AB+BC ……………………………………………….(i)
Now, apply the triangle law of vector addition in the ΔBCDof the parallelogram ABCD as
DB= DC+CB ……………………………………………(ii)
Similarly, from ΔACD, we get
DA= AC+DC
⇒AC= DC−DA …………………………………………(iii)
Now, we know that parallelograms have equal opposites sides and parallel to each other as well. Hence, we get
DA= CB …………………………………………………………(iv)
So, replace DA by CB from equation (iii). Hence, we get equation (iii) as
AC= DC−CB ……………………………………………………..(v)
Now, add equations (ii) and (v), we get
DB+AC= DC+CB+DC−CB
⇒DB+AC= 2DC
⇒DC = 2DB+AC …………………………………………………………..(vi)
Now, subtract the equations (ii) and (v), we get
DB−AC= (DC+CB)−(DC−CB)
DB−AC= DC+CB−DC+CB
DB−AC= 2CB
⇒CB = 2DB−AC ………………………………………………………………………..(vii)
Now, put the values of BD and AC from the problem to the equations (vi) and (vii). Hence, we get
DC = 2i^−3j^+2k^−i^+2j^
DC = 20−j^+2k^= 2−j^+2k^
Similarly, we can get value of CB as
CB = 2(−i^+2j^)−(i^−3j^+2k^)
CB = 2−i^+2j^−i^+3j^−2k^
CB = 2−2i^+5j^−2k^
Now, we can get area of parallelogram of cross-multiplying the adjacent sides DC and CB as given in equation (i).
We know that cross product of two vectors a = a1i^+a2j^+a3k^ and b= b1i^+b2j^+b3k^ is given by the relation
