Question
Question: If the vector <img src="https://cdn.pureessence.tech/canvas_446.png?top_left_x=1144&top_left_y=1385&...
If the vector  satisfying
satisfying  ×
×  + (
+ ( .
. )
) =
=  given by
given by
ma = l +
+  ×
× , then l =
, then l =
A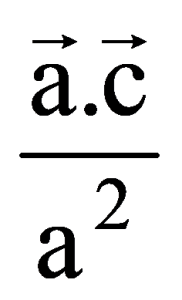
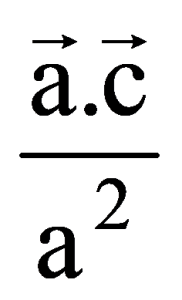
B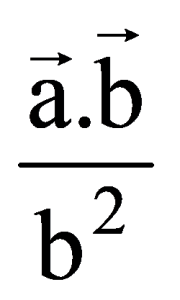
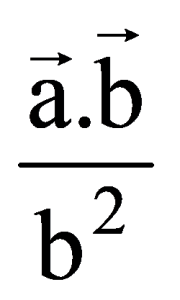
C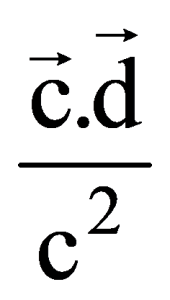
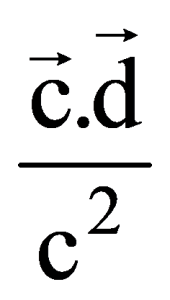
D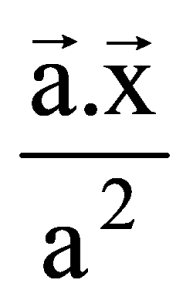
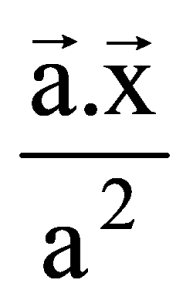
Answer
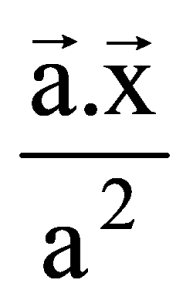
Explanation
Solution
x× a + ( . b ) c = d \ {
. b ) c = d \ { × a + (
× a + ( . b ) c } × c
. b ) c } × c
x= d × c or ( × a ) × c + (
× a ) × c + ( . b ) ( c × c ) = d × c
. b ) ( c × c ) = d × c
x= ( . c ) a – ( a . c )
. c ) a – ( a . c ) = ( d × c ) a × {(
= ( d × c ) a × {( . c ) a –
. c ) a –
x ( a . c ) } = a × ( d × c ) = – ( a . c ) ( a ×
} = a × ( d × c ) = – ( a . c ) ( a × )
)
x= a × ( d × c ) Q a × a = 0  × a = a⋅ca×(d×c)
× a = a⋅ca×(d×c)
a × ( × a ) = a × a⋅ca×(d×c)
× a ) = a × a⋅ca×(d×c)
( a . a ) – ( a .
– ( a . ) a = a × a⋅ca×(d×c)
) a = a × a⋅ca×(d×c)

 = ( a .
= ( a . ) a + a a⋅ca×(d×c)
) a + a a⋅ca×(d×c)
= a2(a⋅x)a + a × 
 = l
= l +
+  ×
× 
Ž l = 
