Solveeit Logo
Login

Question

Question: If the vector a, b and c form the sides BC, CA and AB and equal magnitude respectively of a triangle...

If the vector a, b and c form the sides BC, CA and AB and equal magnitude respectively of a triangle ABC, then
(a) a→.b→+b→.c→+c→.a→=0\overrightarrow{a}.\overrightarrow{b}+\overrightarrow{b}.\overrightarrow{c}+\overrightarrow{c}.\overrightarrow{a}=0
(b) a→×b→=b→×c→=c→×a→\overrightarrow{a}\times \overrightarrow{b}=\overrightarrow{b}\times \overrightarrow{c}=\overrightarrow{c}\times \overrightarrow{a}
(c) a→.b→=b→.c→=c→.a→\overrightarrow{a}.\overrightarrow{b}=\overrightarrow{b}.\overrightarrow{c}=\overrightarrow{c}.\overrightarrow{a}
(d) a→×b→+b→×c→+c→×a→≠0\overrightarrow{a}\times \overrightarrow{b}+\overrightarrow{b}\times \overrightarrow{c}+\overrightarrow{c}\times \overrightarrow{a}\ne 0

Explanation

Solution

Hint: To solve the question given above, we will assume a triangle with all the sides equal. We will take these sides to be equal to some non – zero vectors. Then, we will find the dot and cross product of each side with the other. After doing this, we will check each option one by one.

Complete step-by-step answer:
Before we start the question, we must know what a dot product and cross product in vectors is because in the options given, we have got the cross product and the dot product of two sides. The dot product or scalar product is an algebraic operation that takes two equal length sequences of the vectors and returns a single number. If, a→=x1i^+y1j^ and b→=x2i^+y2j^,\overrightarrow{a}={{x}_{1}}\widehat{i}+{{y}_{1}}\widehat{j}\text{ and }\overrightarrow{b}={{x}_{2}}\widehat{i}+{{y}_{2}}\widehat{j}, then their cross product will be,
a→.b→=(x1i^+y1j^).(x2i^+y2j^)\overrightarrow{a}.\overrightarrow{b}=\left( {{x}_{1}}\widehat{i}+{{y}_{1}}\widehat{j} \right).\left( {{x}_{2}}\widehat{i}+{{y}_{2}}\widehat{j} \right)
a→.b→=x1x2+y1y2\overrightarrow{a}.\overrightarrow{b}={{x}_{1}}{{x}_{2}}+{{y}_{1}}{{y}_{2}}
The dot product is also given by, a→.b→=∣a→∣∣b→∣cos⁡θ.\overrightarrow{a}.\overrightarrow{b}=\left| \overrightarrow{a} \right|\left| \overrightarrow{b} \right|\cos \theta . The cross product of two vectors is defined as a vector that is perpendicular to both the vectors and magnitude equal to the area of the parallelogram. It is given by,
a→×b→=∣a→∣∣b→∣sin⁡θn^\overrightarrow{a}\times \overrightarrow{b}=\left| \overrightarrow{a} \right|\left| \overrightarrow{b} \right|\sin \theta \widehat{n}
Now, we will draw a triangle with the sides represented as a vector.

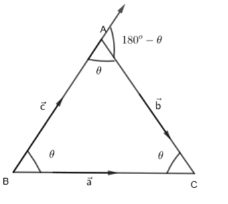
Now, we have drawn a triangle with all its sides equal i.e. it is an equilateral triangle. Thus, all the interior angles of the triangle will be equal to θ=60o.\theta ={{60}^{o}}. Now, as the sides are equal in length, we have,
∣a→∣=∣b→∣=∣c→∣=x\left| \overrightarrow{a} \right|=\left| \overrightarrow{b} \right|=\left| \overrightarrow{c} \right|=x
Now, we will calculate, a→.b→,b→.c→,a→.c→,a→×b→,b→×c→,c→×a→.\overrightarrow{a}.\overrightarrow{b},\overrightarrow{b}.\overrightarrow{c},\overrightarrow{a}.\overrightarrow{c},\overrightarrow{a}\times \overrightarrow{b},\overrightarrow{b}\times \overrightarrow{c},\overrightarrow{c}\times \overrightarrow{a}.
a→.b→=∣a→∣∣b→∣cos⁡θ\overrightarrow{a}.\overrightarrow{b}=\left| \overrightarrow{a} \right|\left| \overrightarrow{b} \right|\cos \theta
⇒a→.b→=x×x×cos⁡60o\Rightarrow \overrightarrow{a}.\overrightarrow{b}=x\times x\times \cos {{60}^{o}}
⇒a→.b→=12x2.....(i)\Rightarrow \overrightarrow{a}.\overrightarrow{b}=\dfrac{1}{2}{{x}^{2}}.....\left( i \right)
b→.c→=∣b→∣∣c→∣cos⁡(180o−θ)\overrightarrow{b}.\overrightarrow{c}=\left| \overrightarrow{b} \right|\left| \overrightarrow{c} \right|\cos \left( {{180}^{o}}-\theta \right)
⇒b→.c→=x×x×cos⁡120o\Rightarrow \overrightarrow{b}.\overrightarrow{c}=x\times x\times \cos {{120}^{o}}
⇒b→.c→=−12x2.....(ii)\Rightarrow \overrightarrow{b}.\overrightarrow{c}=\dfrac{-1}{2}{{x}^{2}}.....\left( ii \right)
a→.c→=∣a→∣∣c→∣cos⁡θ\overrightarrow{a}.\overrightarrow{c}=\left| \overrightarrow{a} \right|\left| \overrightarrow{c} \right|\cos \theta
⇒a→.c→=x×x×cos⁡60o\Rightarrow \overrightarrow{a}.\overrightarrow{c}=x\times x\times \cos {{60}^{o}}
⇒a→.c→=12x2.....(iii)\Rightarrow \overrightarrow{a}.\overrightarrow{c}=\dfrac{1}{2}{{x}^{2}}.....\left( iii \right)
a→×b→=∣a→∣∣b→∣sin⁡θn^\overrightarrow{a}\times \overrightarrow{b}=\left| \overrightarrow{a} \right|\left| \overrightarrow{b} \right|\sin \theta \widehat{n}
⇒a→×b→=x×x×sin⁡60o×n^\Rightarrow \overrightarrow{a}\times \overrightarrow{b}=x\times x\times \sin {{60}^{o}}\times \widehat{n}
⇒a→×b→=32x2n^.....(iv)\Rightarrow \overrightarrow{a}\times \overrightarrow{b}=\dfrac{\sqrt{3}}{2}{{x}^{2}}\widehat{n}.....\left( iv \right)
b→×c→=∣b→∣∣c→∣sin⁡(180o−θ)n^\overrightarrow{b}\times \overrightarrow{c}=\left| \overrightarrow{b} \right|\left| \overrightarrow{c} \right|\sin \left( {{180}^{o}}-\theta \right)\widehat{n}
⇒b→×c=x×x×sin⁡120o×n^\Rightarrow \overrightarrow{b}\times c=x\times x\times \sin {{120}^{o}}\times \widehat{n}
⇒b→×c→=32x2n^.....(v)\Rightarrow \overrightarrow{b}\times \overrightarrow{c}=\dfrac{\sqrt{3}}{2}{{x}^{2}}\widehat{n}.....\left( v \right)
c→×a→=∣c→∣∣a→∣sin⁡θn^\overrightarrow{c}\times \overrightarrow{a}=\left| \overrightarrow{c} \right|\left| \overrightarrow{a} \right|\sin \theta \widehat{n}
⇒c→×a→=x×x×sin⁡60o×n^\Rightarrow \overrightarrow{c}\times \overrightarrow{a}=x\times x\times \sin {{60}^{o}}\times \widehat{n}
⇒c→×a→=32x2n^.....(vi)\Rightarrow \overrightarrow{c}\times \overrightarrow{a}=\dfrac{\sqrt{3}}{2}{{x}^{2}}\widehat{n}.....\left( vi \right)
Option (a): a→.b→+b→.c→+c→.a→=12x2−12x2+12x2=12x2≠0\overrightarrow{a}.\overrightarrow{b}+\overrightarrow{b}.\overrightarrow{c}+\overrightarrow{c}.\overrightarrow{a}=\dfrac{1}{2}{{x}^{2}}-\dfrac{1}{2}{{x}^{2}}+\dfrac{1}{2}{{x}^{2}}=\dfrac{1}{2}{{x}^{2}}\ne 0
So, this option is incorrect.
Option (b): From (iv), (v) and (vi), we have,
a→×b→=b→×c→=c→×a→=32x2n^\overrightarrow{a}\times \overrightarrow{b}=\overrightarrow{b}\times \overrightarrow{c}=\overrightarrow{c}\times \overrightarrow{a}=\dfrac{\sqrt{3}}{2}{{x}^{2}}\widehat{n}
Hence, it is incorrect.
Option (c): From (i), (ii) and (iii), we can see that,
a→.b→=−b→.c→=c→.a→\overrightarrow{a}.\overrightarrow{b}=-\overrightarrow{b}.\overrightarrow{c}=\overrightarrow{c}.\overrightarrow{a}
Hence, it is incorrect.
Option (d): From (iv), (v) and (vi), we get,
a→×b→+b→×c→+c→×a→=32x2n^+32x2n^+32x2n^\overrightarrow{a}\times \overrightarrow{b}+\overrightarrow{b}\times \overrightarrow{c}+\overrightarrow{c}\times \overrightarrow{a}=\dfrac{\sqrt{3}}{2}{{x}^{2}}\widehat{n}+\dfrac{\sqrt{3}}{2}{{x}^{2}}\widehat{n}+\dfrac{\sqrt{3}}{2}{{x}^{2}}\widehat{n}
a→×b→+b→×c→+c→×a→=332x2n^≠0\overrightarrow{a}\times \overrightarrow{b}+\overrightarrow{b}\times \overrightarrow{c}+\overrightarrow{c}\times \overrightarrow{a}=\dfrac{3\sqrt{3}}{2}{{x}^{2}}\widehat{n}\ne 0
Hence, option (d) is the right answer.

Note: In the cross product done inequation (iv), (v) and (vi), one might say that the unit vector n^\widehat{n} will be different for different cross products. The normal vector n^\widehat{n} depends on the vectors of which we have to cross product and as it is an equilateral triangle, the sides are equal, the n^\widehat{n} will be the same for all.