Question

If the variable line $L=y-mx-c=0\left( m,c\in R\text{ and }c\ne 0 \right)$ cuts the curve $y={{x}^{2}}-x$ at P and Q such that $\angle POQ=\dfrac{\pi }{2}$ , where O is the origin, then
(a) $m+c-1=0$
(b) $m-c+1=0$
(c) Line L always passes through $\left( 1,1 \right)$
(d) Line L always passes through $\left( -1,-1 \right)$

Answer 1

Firstly, we have to homogenize the given parabola. For this, we will write the given line in the form $1=\dfrac{y-mx}{c}$ and substitute this for 1 in the given curve for the terms whose degree is less than 2. Since, $\angle POQ=\dfrac{\pi }{2}$ , we will add the coefficient of ${{x}^{2}}$ and the coefficient of ${{y}^{2}}$ in the resulting equation of the previous step and equate it to 0. This step will give an equation. To check whether options c and are true, we will substitute the points given in options c and d in the given line and check whether the resultant value is equal to the equation we obtained.

Complete step by step answer:
We are given that the line $L=y-mx-c=0$ cuts the curve $y={{x}^{2}}-x$ at P and Q such that $\angle POQ=\dfrac{\pi }{2}$ where O is the origin. Let us graph this situation.

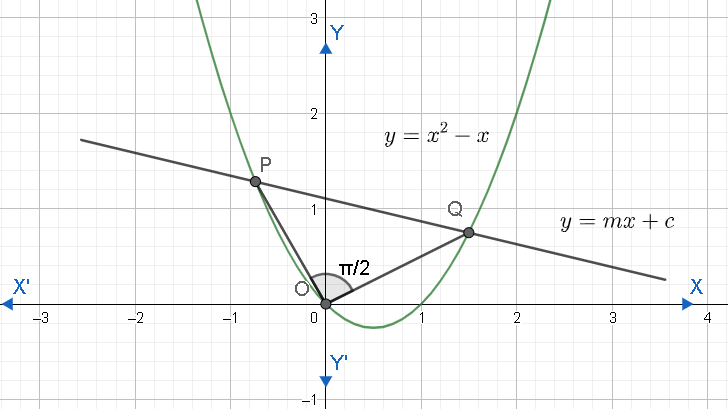
We can write $L=y-mx-c=0$ as
$y=mx+c$
Let us move mx to the LHS.
$\Rightarrow y-mx=c$
We can write the above equation as
$\Rightarrow y-mx=c\times 1$
Let us take c to the LHS.
$\begin{aligned} & \Rightarrow \dfrac{y-mx}{c}=1 \\\ & \Rightarrow 1=\dfrac{y-mx}{c}...\left( i \right) \\\ \end{aligned}$
We can write the given parabola $y={{x}^{2}}-x$ as
$y-{{x}^{2}}+x=0$
Now, let us homogenize this parabola. We can do this by rewriting the above parabola as
$\Rightarrow y\times 1-{{x}^{2}}+x\times 1=0$
Let us substitute (i) in the above equation.
$\Rightarrow y\left( \dfrac{y-mx}{c} \right)-{{x}^{2}}+x\left( \dfrac{y-mx}{c} \right)=0$
We have to apply distributive property on the LHS.
$\Rightarrow \dfrac{{{y}^{2}}-ymx}{c}-{{x}^{2}}+\dfrac{xy-m{{x}^{2}}}{c}=0$
Now, we have to take the LCM and simplify.
$\begin{aligned} & \Rightarrow \dfrac{{{y}^{2}}-ymx}{c}-\dfrac{c{{x}^{2}}}{c}+\dfrac{xy-m{{x}^{2}}}{c}=0 \\\ & \Rightarrow \dfrac{1}{c}\left( {{y}^{2}}-ymx-c{{x}^{2}}+xy-m{{x}^{2}} \right)=0 \\\ \end{aligned}$
Let us take c to the RHS.
$\begin{aligned} & \Rightarrow {{y}^{2}}-ymx-c{{x}^{2}}+xy-m{{x}^{2}}=0\times c \\\ & \Rightarrow {{y}^{2}}-ymx-c{{x}^{2}}+xy-m{{x}^{2}}=0 \\\ \end{aligned}$
Let us take the common terms outside.
$\Rightarrow \left( -c-m \right){{x}^{2}}+{{y}^{2}}+xy\left( 1-m \right)=0...\left( i \right)$
We are given that $\angle POQ=\dfrac{\pi }{2}$ . Therefore, the sum of coefficient of ${{x}^{2}}$ and the coefficient of ${{y}^{2}}$ will be equal to 0. From (i), we can see that the coefficient of ${{x}^{2}}$ is $-c-m$ and that of ${{y}^{2}}$ is 1. Therefore, we can write
$\Rightarrow -c-m+1=0$
Let us take –c and –m to the RHS.
$\Rightarrow 1=c+m$
Now, we have to take 1 to the RHS.
$\Rightarrow c+m-1=0...\left( ii \right)$
Therefore, option (a) is correct and option b will not be satisfied.
We can check whether option c is correct or not. Let us substitute the point $\left( 1,1 \right)$ in the given line L and check whether it is equal to the equation (ii).
$\begin{aligned} & \Rightarrow L=y-mx-c=0 \\\ & \Rightarrow 1-m\times 1-c=0 \\\ & \Rightarrow 1-m-c=0 \\\ & \Rightarrow m+c-1=0 \\\ \end{aligned}$
Therefore, option c is correct.
Now, let us check whether option d is correct or not by substituting the point $\left( -1,-1 \right)$ in the given line L.
$\begin{aligned} & \Rightarrow L=y-mx-c=0 \\\ & \Rightarrow -1-m\times -1-c=0 \\\ & \Rightarrow -1+m-c=0 \\\ & \Rightarrow -m+c+1=0 \\\ \end{aligned}$
Therefore, option d is incorrect.
So, the correct answer is “Option a and c”.

Note: Students must be able to homogenize a curve. Homogenization is the process of converting the terms to a similar degree. This is the reason why we did not substitute for 1 in ${{x}^{2}}$ terms of the given term. We converted the other terms to degree 2. Students have a chance of making a mistake by equating the sum of coefficients of ${{x}^{2}}$ and the coefficient of ${{y}^{2}}$ to 1.