Question

If the value of x satisfying the equation $\sin^{-1}\sqrt{1-x^2}=\tan^{-1}\sqrt{\frac{2}{x}-1}$ is $\frac{a}{b}$ (where a and b are coprime), then the value of $a^2 + b^2$ is

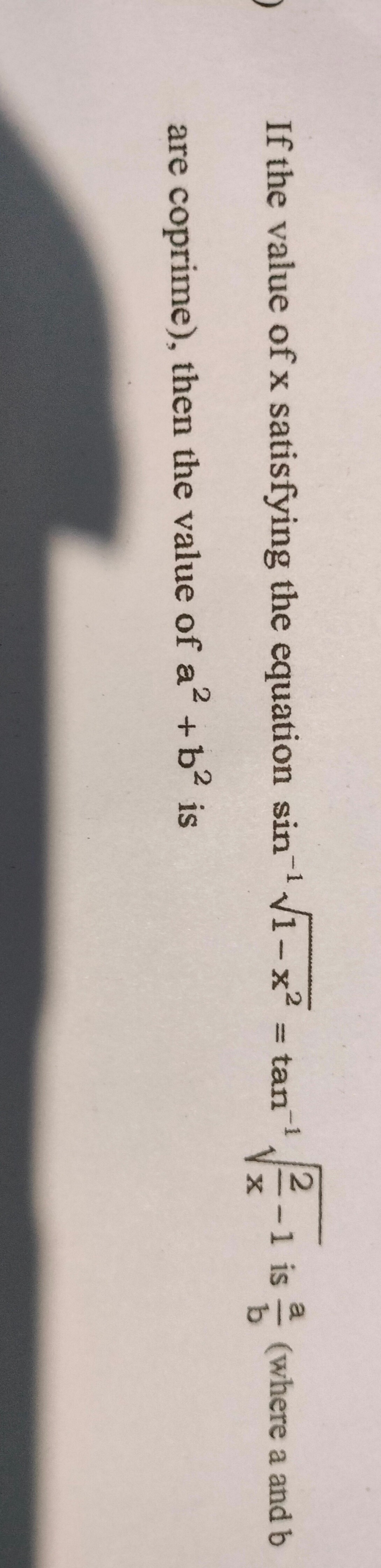
Answer 1

5

Answer 2

Given:

$$\sin^{-1}\sqrt{1-x^2} = \tan^{-1}\sqrt{\frac{2}{x}-1}$$

Let $\theta = \sin^{-1}\sqrt{1-x^2}$. Then:

$$\sin\theta = \sqrt{1-x^2} \quad \text{and} \quad \cos\theta = x \quad (\text{since } x>0)$$

Thus,

$$\tan\theta = \frac{\sin\theta}{\cos\theta} = \frac{\sqrt{1-x^2}}{x}.$$

On the right-hand side, if we set $\phi = \tan^{-1}\sqrt{\frac{2}{x}-1}$, then:

$$\tan\phi = \sqrt{\frac{2}{x}-1}.$$

Since the equation equates the angles, we have $\theta = \phi$, so:

$$\frac{\sqrt{1-x^2}}{x} = \sqrt{\frac{2}{x}-1}.$$

Squaring both sides:

$$\frac{1-x^2}{x^2} = \frac{2}{x}-1.$$

Multiply both sides by $x^2$:

$$1 - x^2 = 2x - x^2.$$

Cancel $-x^2$ from both sides:

$$1 = 2x \quad \Rightarrow \quad x = \frac{1}{2}.$$

Since $x=\frac{a}{b}=\frac{1}{2}$ with $a=1$ and $b=2$, we compute:

$$a^2 + b^2 = 1^2 + 2^2 = 1 + 4 = 5.$$