Question

If the value of x satisfying the equation $\sin^{-1}\sqrt{1-x^2}=\tan^{-1}\sqrt{\frac{2}{x}-1}$ is $\frac{a}{b}$ (where a and b are coprime), then the value of $a^2 + b^2$ is

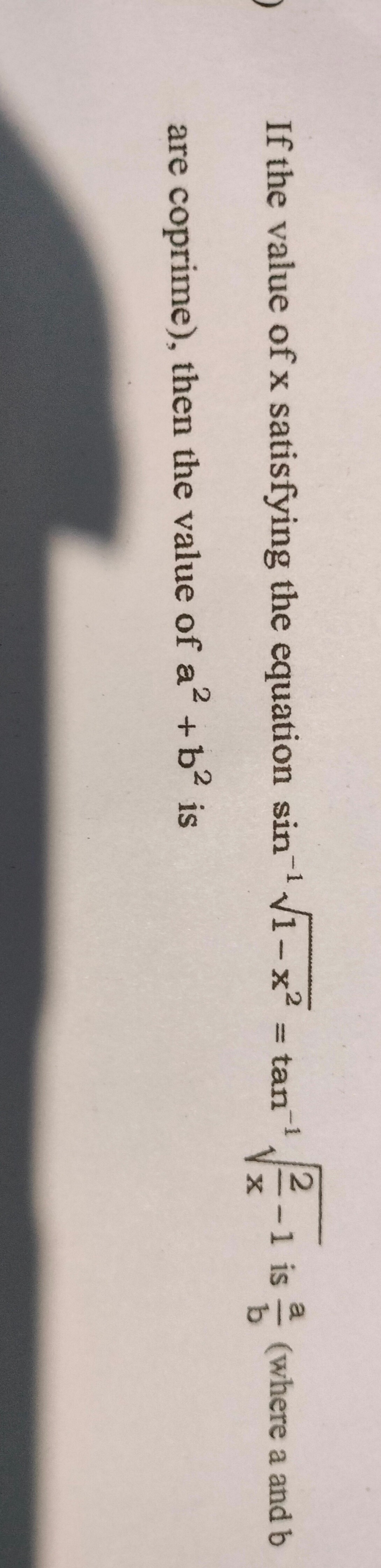
Answer 1

5

Answer 2

Solution:

Given the equation:

$$\sin^{-1}\sqrt{1-x^2}=\tan^{-1}\sqrt{\frac{2}{x}-1}$$

1. Substitution: Let $x = \cos\theta$ (with $0 \leq \theta \leq \frac{\pi}{2}$), so that

   $$\sqrt{1-x^2} = \sin\theta.$$

   Hence, the left side becomes:

   $$\sin^{-1}(\sin\theta)=\theta.$$

2. Rewrite the Equation: Then the equation becomes:

   $$\theta=\tan^{-1}\sqrt{\frac{2}{\cos\theta}-1}.$$

   Taking the tangent on both sides:

   $$\tan\theta=\sqrt{\frac{2}{\cos\theta}-1}.$$

3. Express $\tan\theta$: But $\tan\theta=\frac{\sin\theta}{\cos\theta}=\frac{\sqrt{1-\cos^2\theta}}{\cos\theta}$. Hence:

   $$\frac{\sqrt{1-\cos^2\theta}}{\cos\theta}=\sqrt{\frac{2}{\cos\theta}-1}.$$

4. Square Both Sides: Squaring gives:

   $$\frac{1-\cos^2\theta}{\cos^2\theta}=\frac{2}{\cos\theta}-1.$$

   Multiply both sides by $\cos^2\theta$:

   $$1-\cos^2\theta=2\cos\theta-\cos^2\theta.$$

5. Solve for $\cos\theta$: Cancel $-\cos^2\theta$ from both sides:

   $$1=2\cos\theta \quad\Longrightarrow\quad \cos\theta=\frac{1}{2}.$$

   Since $x=\cos\theta$, we obtain:

   $$x=\frac{1}{2}.$$

6. Final Step: Writing $x=\frac{a}{b}$ with $a$ and $b$ coprime gives $a=1$ and $b=2$. Then:

   $$a^2+b^2=1^2+2^2=1+4=5.$$