Question

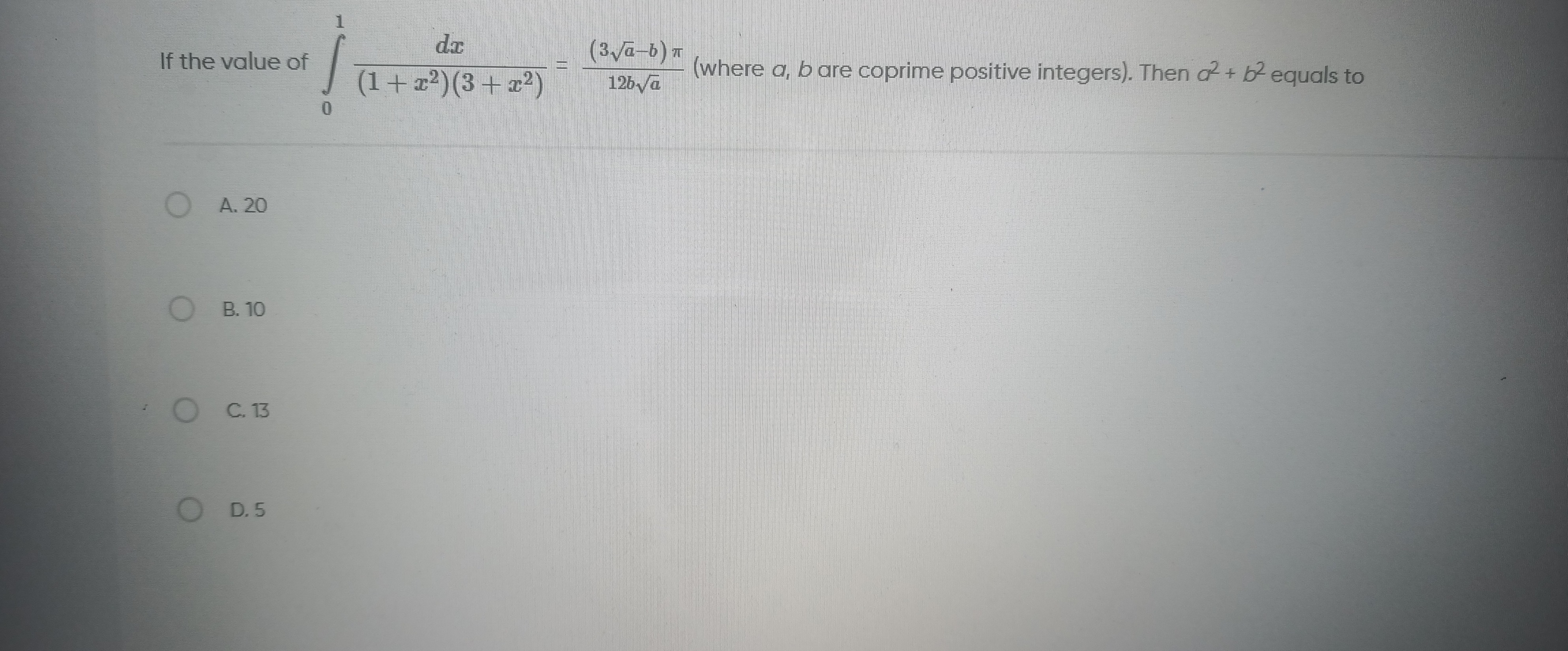
If the value of $\int_{0}^{1} \frac{dx}{(1+x^2)(3+x^2)} = \frac{(3\sqrt{a}-b)\pi}{12b\sqrt{a}}$ (where a, b are coprime positive integers). Then $a^2 + b^2$ equals to

• A. 20
• B. 10
• C. 13
• D. 5

Answer 1

Answer: (C)

13

Answer 2

The integral is evaluated using partial fractions. Let $y=x^2$, then $\frac{1}{(1+y)(3+y)} = \frac{1}{2}\left(\frac{1}{1+y} - \frac{1}{3+y}\right)$. So the integral becomes $\frac{1}{2} \int_{0}^{1} \left(\frac{1}{1+x^2} - \frac{1}{3+x^2}\right) dx$. This evaluates to $\frac{1}{2} \left[ \arctan(x) - \frac{1}{\sqrt{3}}\arctan\left(\frac{x}{\sqrt{3}}\right) \right]_{0}^{1} = \frac{1}{2} \left( \frac{\pi}{4} - \frac{1}{\sqrt{3}}\frac{\pi}{6} \right) = \frac{\pi}{8} - \frac{\pi}{12\sqrt{3}}$. Rationalizing the second term gives $\frac{\pi}{8} - \frac{\pi\sqrt{3}}{36}$. The given form is $\frac{(3\sqrt{a}-b)\pi}{12b\sqrt{a}} = \frac{3\sqrt{a}\pi}{12b\sqrt{a}} - \frac{b\pi}{12b\sqrt{a}} = \frac{\pi}{4b} - \frac{\pi}{12\sqrt{a}}$. Equating the two forms: $\frac{\pi}{8} - \frac{\pi\sqrt{3}}{36} = \frac{\pi}{4b} - \frac{\pi}{12\sqrt{a}}$. Comparing terms, $\frac{1}{8} = \frac{1}{4b} \implies b=2$, and $\frac{\sqrt{3}}{36} = \frac{1}{12\sqrt{a}} \implies 12\sqrt{3a} = 36 \implies \sqrt{3a} = 3 \implies 3a = 9 \implies a=3$. Since $a=3$ and $b=2$ are coprime positive integers, $a^2 + b^2 = 3^2 + 2^2 = 9+4=13$.