Solveeit Logo
Login

Question

Question: If the value of $(2020)^2 + \frac{(2021)^2}{1!} + \frac{(2022)^2}{2!} + \frac{(2023)^2}{3!} + \dots$...

If the value of (2020)2+(2021)21!+(2022)22!+(2023)23!+…(2020)^2 + \frac{(2021)^2}{1!} + \frac{(2022)^2}{2!} + \frac{(2023)^2}{3!} + \dots is

Answer

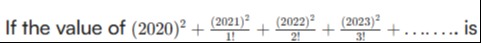
4084442e

Explanation

Solution

The given series is S=(2020)2+(2021)21!+(2022)22!+(2023)23!+…S = (2020)^2 + \frac{(2021)^2}{1!} + \frac{(2022)^2}{2!} + \frac{(2023)^2}{3!} + \dots. Let n=2020n = 2020. The series can be written as: S=∑k=0∞(n+k)2k!S = \sum_{k=0}^{\infty} \frac{(n+k)^2}{k!} Expanding (n+k)2(n+k)^2: (n+k)2=n2+2nk+k2(n+k)^2 = n^2 + 2nk + k^2 Substituting this into the summation: S=∑k=0∞n2+2nk+k2k!S = \sum_{k=0}^{\infty} \frac{n^2 + 2nk + k^2}{k!} Splitting the sum: S=∑k=0∞n2k!+∑k=0∞2nkk!+∑k=0∞k2k!S = \sum_{k=0}^{\infty} \frac{n^2}{k!} + \sum_{k=0}^{\infty} \frac{2nk}{k!} + \sum_{k=0}^{\infty} \frac{k^2}{k!} S=n2∑k=0∞1k!+2n∑k=0∞kk!+∑k=0∞k2k!S = n^2 \sum_{k=0}^{\infty} \frac{1}{k!} + 2n \sum_{k=0}^{\infty} \frac{k}{k!} + \sum_{k=0}^{\infty} \frac{k^2}{k!} We know that ∑k=0∞1k!=e\sum_{k=0}^{\infty} \frac{1}{k!} = e. For the second term: ∑k=0∞kk!=∑k=1∞kk(k−1)!=∑k=1∞1(k−1)!=∑j=0∞1j!=e\sum_{k=0}^{\infty} \frac{k}{k!} = \sum_{k=1}^{\infty} \frac{k}{k(k-1)!} = \sum_{k=1}^{\infty} \frac{1}{(k-1)!} = \sum_{j=0}^{\infty} \frac{1}{j!} = e. For the third term: ∑k=0∞k2k!=∑k=0∞k(k−1)+kk!=∑k=0∞k(k−1)k!+∑k=0∞kk!\sum_{k=0}^{\infty} \frac{k^2}{k!} = \sum_{k=0}^{\infty} \frac{k(k-1) + k}{k!} = \sum_{k=0}^{\infty} \frac{k(k-1)}{k!} + \sum_{k=0}^{\infty} \frac{k}{k!}. ∑k=0∞k(k−1)k!=∑k=2∞k(k−1)k(k−1)(k−2)!=∑k=2∞1(k−2)!=∑j=0∞1j!=e\sum_{k=0}^{\infty} \frac{k(k-1)}{k!} = \sum_{k=2}^{\infty} \frac{k(k-1)}{k(k-1)(k-2)!} = \sum_{k=2}^{\infty} \frac{1}{(k-2)!} = \sum_{j=0}^{\infty} \frac{1}{j!} = e. So, ∑k=0∞k2k!=e+e=2e\sum_{k=0}^{\infty} \frac{k^2}{k!} = e + e = 2e. Substituting these values back into the expression for SS: S=n2(e)+2n(e)+2e=e(n2+2n+2)S = n^2(e) + 2n(e) + 2e = e(n^2 + 2n + 2) Given n=2020n=2020: S=e((2020)2+2(2020)+2)=e(4080400+4040+2)=e(4084442)S = e((2020)^2 + 2(2020) + 2) = e(4080400 + 4040 + 2) = e(4084442) Thus, the value of the series is 4084442e4084442e.