Question

If the trigonometric equation $\sin \left( x \right)=0.5$, how do you find the value of x?

Answer 1

We first find the principal value of x for which $\sin \left( x \right)=0.5=\dfrac{1}{2}$. In that domain, equal value of the same ratio gives equal angles. We find the angle value for x. At the end we also find the general solution for the equation $\sin \left( x \right)=0.5$.

Complete step-by-step solution:
It’s given that $\sin \left( x \right)=0.5$. The value in fraction is $\dfrac{1}{2}$. We need to find x for which $\sin \left( x \right)=\dfrac{1}{2}$.
We know that in the principal domain or the periodic value of $-\dfrac{\pi }{2}\le x\le \dfrac{\pi }{2}$ for $\sin x$, if we get $\sin a=\sin b$ where $-\dfrac{\pi }{2}\le a,b\le \dfrac{\pi }{2}$ then $a=b$.
We have the value of $\sin \left( \dfrac{\pi }{6} \right)$ as $\dfrac{1}{2}$. $-\dfrac{\pi }{2} < \dfrac{\pi }{6} < \dfrac{\pi }{2}$.
Therefore, $\sin \left( x \right)=\dfrac{1}{2}=\sin \left( \dfrac{\pi }{6} \right)$ which gives $x=\dfrac{\pi }{6}$.
For $\sin \left( x \right)=0.5$, the value of x is $x=\dfrac{\pi }{6}$.
We also can show the solutions (primary and general) of the equation $\sin \left( x \right)=0.5$ through the graph. We take $y=\sin \left( x \right)=0.5$. We got two equations $y=\sin \left( x \right)$ and $y=0.5$. We place them on the graph and find the solutions as their intersecting points.

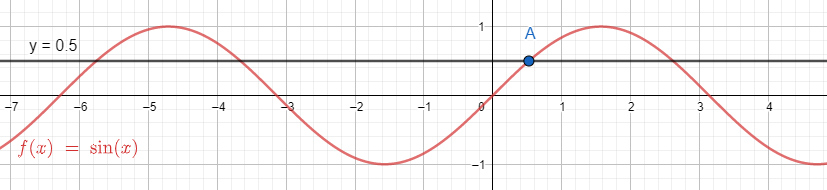
We can see the primary solution in the interval $-\dfrac{\pi }{2}\le x\le \dfrac{\pi }{2}$ is the point A as $x=\dfrac{\pi }{6}$.
All the other intersecting points of the curve and the line are general solutions.

Note: Although for elementary knowledge the principal domain is enough to solve the problem. But if mentioned to find the general solution then the domain changes to $-\infty \le x\le \infty$. In that case we have to use the formula $x=n\pi +{{\left( -1 \right)}^{n}}a$ for $\sin \left( x \right)=\sin a$ where $-\dfrac{\pi }{2}\le a\le \dfrac{\pi }{2}$. For our given problem $\sin \left( x \right)=0.5=\dfrac{1}{2}$, the general solution will be $x=n\pi +{{\left( -1 \right)}^{n}}\dfrac{\pi }{6}$. Here $n\in \mathbb{Z}$.