Question

If the total surface area of a cone is given, its volume is maximum when the semi vertical angle is
(a) ${{\sin }^{-1}}\dfrac{1}{3}$
(b) ${{\sin }^{-1}}\dfrac{1}{\sqrt{3}}$
(c) ${{\tan }^{-1}}\dfrac{1}{3}$
(d) ${{\tan }^{-1}}\dfrac{1}{\sqrt{3}}$

Answer 1

To maximize a variable quantity, we first convert it and make it a function of a single variable. Then we will differentiate it with respect to that variable to get the value of the variable when the function gets to an extreme point. We will use the following formulae,
The volume of a cone is $V=\dfrac{1}{3}\pi {{r}^{2}}h$ where r is the radius of the base of the cone and h is the height of the cone.
The total surface area of a cone is $TSA=\pi rl+\pi {{r}^{2}}$ where l is the slant height of the cone and r is the radius of the base of the cone.
We have to find the semi vertical angle of the cone with maximum volume and given total surface area. We will sketch a rough diagram.

Complete step by step answer:

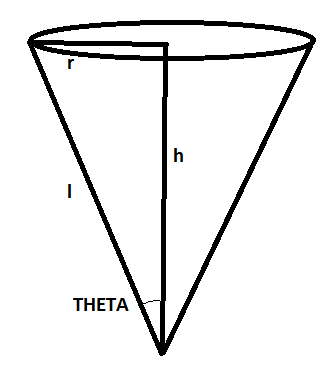
Now, as the total surface area of the cone is given, so, we can write the following
$TSA=p=\pi rl+\pi {{r}^{2}}$ where p is a constant.
We also know that the slant height of a cone can be written as ${{l}^{2}}={{r}^{2}}+{{h}^{2}}$ where r is the radius of the cone, l is the slant height of the cone and h is the height of the cone.
Now, we can write the TSA as follows
$\begin{aligned} & p=\pi rl+\pi {{r}^{2}} \\\ & p-\pi {{r}^{2}}=\pi rl \\\ \end{aligned}$
On squaring the expression, we get
${{\pi }^{2}}{{r}^{2}}{{l}^{2}}={{\left( p-\pi {{r}^{2}} \right)}^{2}}....(a)$
Now, we will substitute the value of $h=\sqrt{{{l}^{2}}-{{r}^{2}}}$ in the formula for the volume of the cone. So now we get,
$Volume=\dfrac{1}{3}\pi {{r}^{2}}\left( \sqrt{{{l}^{2}}-{{r}^{2}}} \right)$
Now, we will rearrange the above equation by shifting $\pi$ and $r$ inside the square root in the following manner,
$\begin{aligned} & Volume=\dfrac{1}{3}r\left( \sqrt{{{\pi }^{2}}{{r}^{2}}{{l}^{2}}-{{\pi }^{2}}{{r}^{2}}\cdot {{r}^{2}}} \right) \\\ & =\dfrac{1}{3}r\left( \sqrt{{{\pi }^{2}}{{r}^{2}}{{l}^{2}}-{{\pi }^{2}}{{r}^{4}}} \right) \end{aligned}$
Now, using equation (a), we will substitute the value of ${{\pi }^{2}}{{r}^{2}}{{l}^{2}}={{\left( p-\pi {{r}^{2}} \right)}^{2}}$ in the above expression. We get the following,
$\begin{aligned} & Volume\left( V \right)=\dfrac{1}{3}r\left( \sqrt{{{\left( p-\pi {{r}^{2}} \right)}^{2}}-{{\pi }^{2}}{{r}^{4}}} \right) \\\ & =\dfrac{1}{3}r\left( \sqrt{{{p}^{2}}-2p\pi {{r}^{2}}+{{\pi }^{2}}{{r}^{4}}-{{\pi }^{2}}{{r}^{4}}} \right) \\\ & =\dfrac{1}{3}r\left( \sqrt{{{p}^{2}}-2p\pi {{r}^{2}}} \right) \end{aligned}$
Now, we will differentiate the volume with respect to the variable $r$. So, we have

& \dfrac{dV}{dr}=\dfrac{d}{dr}\left( \dfrac{1}{3}r\left( \sqrt{{{p}^{2}}-2p\pi {{r}^{2}}} \right) \right) \\\ & =\dfrac{1}{3}\dfrac{d}{dr}\left( r\left( \sqrt{{{p}^{2}}-2p\pi {{r}^{2}}} \right) \right) \end{aligned}$$ For the differentiation of product of two functions $f$ and $g$, we know that $\dfrac{d\left( f\cdot g \right)}{dx}=f\cdot \dfrac{dg}{dx}+g\cdot \dfrac{df}{dx}$ . Using this formula in the differentiation of the volume, we get $\dfrac{dV}{dr}=\dfrac{1}{3}\left[ r\cdot \dfrac{d\left( \sqrt{{{p}^{2}}-2p\pi {{r}^{2}}} \right)}{dr}+\left( \sqrt{{{p}^{2}}-2p\pi {{r}^{2}}} \right)\cdot \dfrac{d\left( r \right)}{dr} \right]$ Simplifying the above equation, we get the following, $\begin{aligned} & \dfrac{dV}{dr}=\dfrac{1}{3}\left[ r\cdot \dfrac{1\times \left( -2p\pi \times 2r \right)}{2\sqrt{{{p}^{2}}-2p\pi {{r}^{2}}}}+\left( \sqrt{{{p}^{2}}-2p\pi {{r}^{2}}} \right) \right] \\\ & =\dfrac{1}{3}\left[ r\cdot \dfrac{-4p\pi r}{2\sqrt{{{p}^{2}}-2p\pi {{r}^{2}}}}+\left( \sqrt{{{p}^{2}}-2p\pi {{r}^{2}}} \right) \right] \\\ & =\dfrac{1}{3}\left[ \dfrac{-2p\pi {{r}^{2}}}{\sqrt{{{p}^{2}}-2p\pi {{r}^{2}}}}+\left( \sqrt{{{p}^{2}}-2p\pi {{r}^{2}}} \right) \right] \\\ & =\dfrac{1}{3}\left[ \dfrac{-2p\pi {{r}^{2}}+{{p}^{2}}-2p\pi {{r}^{2}}}{\sqrt{{{p}^{2}}-2p\pi {{r}^{2}}}} \right] \\\ & =\dfrac{1}{3}\left[ \dfrac{{{p}^{2}}-4p\pi {{r}^{2}}}{\sqrt{{{p}^{2}}-2p\pi {{r}^{2}}}} \right] \end{aligned}$ To maximize the volume, we will equate the differentiation of the volume to 0. We will solve $\dfrac{dV}{dr}=0$. Substituting the value of $\dfrac{dV}{dr}$ from the above equation, we get $\dfrac{1}{3}\left[ \dfrac{{{p}^{2}}-4p\pi {{r}^{2}}}{\sqrt{{{p}^{2}}-2p\pi {{r}^{2}}}} \right]=0$ As the denominator in the above equation cannot be 0, we have ${{p}^{2}}-4p\pi {{r}^{2}}=0$. Since $p\ne 0$, we get $p=4\pi {{r}^{2}}$. Now, substituting this value of p in equation (a), we get ${{\pi }^{2}}{{r}^{2}}{{l}^{2}}={{\left( 4\pi {{r}^{2}}-\pi {{r}^{2}} \right)}^{2}}$ Simplifying this equation we get, $\begin{aligned} & {{\pi }^{2}}{{r}^{2}}{{l}^{2}}={{\left( 3\pi {{r}^{2}} \right)}^{2}} \\\ & {{\pi }^{2}}{{r}^{2}}{{l}^{2}}=9{{\pi }^{2}}{{r}^{4}} \\\ & \therefore \dfrac{{{r}^{2}}}{{{l}^{2}}}=\dfrac{1}{9} \\\ & \therefore \dfrac{r}{l}=\dfrac{1}{3} \\\ \end{aligned}$ Now, as we can see in the figure, we can write $\sin \theta =\dfrac{r}{l}=\dfrac{1}{3}$. Therefore, the semi vertical angle is $\theta ={{\sin }^{-1}}\dfrac{1}{3}$. **So, the correct answer is “Option a”.** **Note:** This process works as any function attains its maximum or minimum value at the point where its derivative becomes 0. In order to find which value of x is maxima or minima, we need to calculate the double derivative of the function in which, on putting these values that are/is obtained on equating the first derivative with 0, we can get the maxima or minima by looking at the value of the double derivative. If the value of the double derivative is positive, then it is minima. If the value turns out to be negative, then it is maxima.