Solveeit Logo
Login

Question

Question: If the tangent at the point P of a standard ellipse meets the axes in T and t and \[C{{Y}_{1}}\] is ...

If the tangent at the point P of a standard ellipse meets the axes in T and t and CY1C{{Y}_{1}} is the perpendicular on it from the centre then.
a)TtPY1=a2−b2a)TtP{{Y}_{1}}={{a}^{2}}-{{b}^{2}}
b) least value of Tt is a+bb)\text{ least value of Tt is }a+b

Explanation

Solution

Now first we will consider any point P = (acos⁡θ,asin⁡θ)\left( a\cos \theta ,a\sin \theta \right) on ellipse. Now we will find the equation of tangent passing through P. Now once we have the equation of tangent we will find the coordinates of T and t by substituting x = 0 and y = 0. Now with the help of this we will find the slope of the tangent. Hence we know that slope of the line perpendicular to the tangent as for the perpendicular line we have m1m2=−1{{m}_{1}}{{m}_{2}}=-1 . Now once we have equation of line CY1C{{Y}_{1}} we can say that the distance PY1P{{Y}_{1}} is perpendicular distance from point P to CY1C{{Y}_{1}}. Hence we have distance PY1P{{Y}_{1}} . We can find length Tt as we know the Coordinates of T and t hence we can find the minimum value of Tt as well as PY1P{{Y}_{1}} .

Complete step by step answer:
Now first let us consider an ellipse
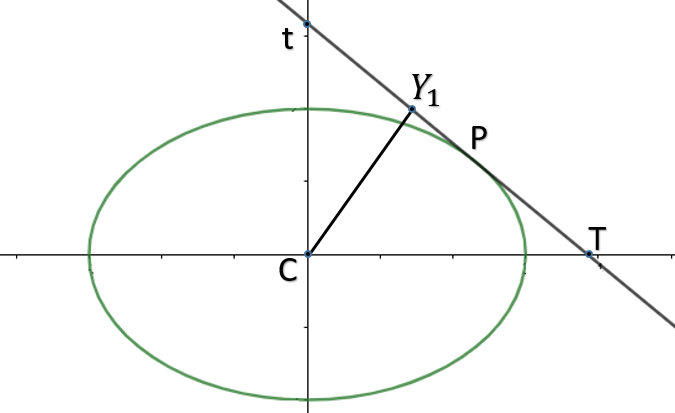
Let a Tangent be drawn at point P.
The tangent meets x-axis at T and y-axis at t.
CY1C{{Y}_{1}} is perpendicular on it from the centre.
Let us draw a figure of the following.

Now we know that equation of ellipse is x2a2+y2b2=1\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1
Now equation of tangent at any point (x1,y1)\left( {{x}_{1}},{{y}_{1}} \right) on ellipse is given by
xx1a2+yy1b2=1\dfrac{x{{x}_{1}}}{{{a}^{2}}}+\dfrac{y{{y}_{1}}}{{{b}^{2}}}=1
Now let us say point P is (acos⁡θ,asin⁡θ)\left( a\cos \theta ,a\sin \theta \right) hence we get the equation of tangent at this point is
xacos⁡θa2+ybsin⁡θb2=1 ⇒xcos⁡θa+ysin⁡θb=1 \begin{aligned} & \dfrac{xa\cos \theta }{{{a}^{2}}}+\dfrac{yb\sin \theta }{{{b}^{2}}}=1 \\\ & \Rightarrow \dfrac{x\cos \theta }{a}+\dfrac{y\sin \theta }{b}=1 \\\ \end{aligned}

Hence the equation of tangent is xcos⁡θa+ysin⁡θb=1..........................(1)\dfrac{x\cos \theta }{a}+\dfrac{y\sin \theta }{b}=1..........................\left( 1 \right)
Now let us find the coordinates of T and t
Now we know that T lies on x-axis as well as on the tangent.
Hence if we substitute y = 0 in (1) we will get coordinates of T
xcos⁡θa+(0)sin⁡θb=1 ⇒xcos⁡θa=1 ⇒xcos⁡θ=a \begin{aligned} & \dfrac{x\cos \theta }{a}+\dfrac{\left( 0 \right)\sin \theta }{b}=1 \\\ & \Rightarrow \dfrac{x\cos \theta }{a}=1 \\\ & \Rightarrow x\cos \theta =a \\\ \end{aligned}
Now dividing the equation by cos⁡θ\cos \theta and using sec⁡θ=1cos⁡θ\sec \theta =\dfrac{1}{\cos \theta } we get
x=asec⁡θx=a\sec \theta
Hence coordinate of T is (asec⁡θ,0)\left( a\sec \theta ,0 \right)
Now t lies on Y axis and on the tangent
Hence substituting x = 0 in equation (1) we get
(0)cos⁡θa+ysin⁡θb=1 ⇒ysin⁡θb=1 ⇒ysin⁡θ=b \begin{aligned} & \dfrac{\left( 0 \right)\cos \theta }{a}+\dfrac{y\sin \theta }{b}=1 \\\ & \Rightarrow \dfrac{y\sin \theta }{b}=1 \\\ & \Rightarrow y\sin \theta =b \\\ \end{aligned}
Now dividing by sin⁡θ\sin \theta and using cos⁡ecθ=1sin⁡θ\cos ec\theta =\dfrac{1}{\sin \theta } we get
y=bcos⁡ecθy=b\cos ec\theta
Hence coordinates of t is (0,bcos⁡ecθ)\left( 0,b\cos ec\theta \right) .
Now we have T = (asec⁡θ,0)\left( a\sec \theta ,0 \right) and t is (0,bcos⁡ecθ)\left( 0,b\cos ec\theta \right)
Now again consider the equation of tangent xcos⁡θa+ysin⁡θb=1\dfrac{x\cos \theta }{a}+\dfrac{y\sin \theta }{b}=1
Now let us convert the equation in form of y = mx + c.

ysin⁡θb=1−xcos⁡θa\dfrac{y\sin \theta }{b}=1-\dfrac{x\cos \theta }{a}

& \Rightarrow y\sin \theta =b-\dfrac{bx\cos \theta }{a} \\\ & \Rightarrow y=\dfrac{b}{\sin \theta }-\dfrac{bx\cos \theta }{a\sin \theta } \\\ \end{aligned}$$ Now we have the slope of this line is $-\dfrac{b\cos \theta }{a\sin \theta }$ Now we know that if ${{m}_{1}},{{m}_{2}}$ are slopes of two perpendicular lines then ${{m}_{1}}{{m}_{2}}=-1$ And we have line $$C{{Y}_{1}}$$ is perpendicular to tangent hence its slope will be $\dfrac{a\sin \theta }{b\cos \theta }$ Now we know that the line $$C{{Y}_{1}}$$ passes through centre that is (0, 0) and slope of line is $\dfrac{a\sin \theta }{b\cos \theta }$ Hence the equation of line $$C{{Y}_{1}}$$ in slope-point form is given by $$y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$$ Hence we get equation of line $$C{{Y}_{1}}$$ is $\begin{aligned} & y-0=\dfrac{a\sin \theta }{b\cos \theta }\left( x-0 \right) \\\ & y=\dfrac{a\sin \theta }{b\cos \theta }x \\\ & by\cos \theta =xa\sin \theta \\\ & by\cos \theta -ax\sin \theta =0 \\\ \end{aligned}$ Now Consider $$P{{Y}_{1}}$$ . $$P{{Y}_{1}}$$ is nothing but perpendicular distance from point P on line $$C{{Y}_{1}}$$ Now we know that perpendicular distance from point $\left( {{x}_{1}},{{y}_{1}} \right)$ on line ax + by = 0 is given by $\left| \dfrac{a{{x}_{1}}+b{{y}_{1}}}{\sqrt{{{a}^{2}}+{{b}^{2}}}} \right|$ Now point P is$\left( a\cos \theta ,a\sin \theta \right)$ and line $$C{{Y}_{1}}$$ is $by\cos \theta -ax\sin \theta =0$ Hence we get the distance $$P{{Y}_{1}}$$ is equal to $\begin{aligned} & \left| \dfrac{{{a}^{2}}\sin \theta \cos \theta -{{b}^{2}}\cos \theta \sin \theta }{\sqrt{{{\left( a\sin \theta \right)}^{2}}+{{\left( b\cos \theta \right)}^{2}}}} \right| \\\ & =\dfrac{\left( {{a}^{2}}-{{b}^{2}} \right)\sin \theta \cos \theta }{\sqrt{{{a}^{2}}{{\sin }^{2}}\theta +{{b}^{2}}{{\cos }^{2}}\theta }}...............................\left( 2 \right) \\\ \end{aligned}$ Now we have T = $\left( a\sec \theta ,0 \right)$ and t is $\left( 0,b\cos ec\theta \right)$ Now by distance formula we get $$\begin{aligned} & Tt=\sqrt{{{\left( a\sec \theta \right)}^{2}}+{{\left( b\cos ec\theta \right)}^{2}}} \\\ & Tt=\sqrt{{{a}^{2}}{{\sec }^{2}}\theta +{{b}^{2}}\cos e{{c}^{2}}\theta } \\\ & Tt=\sqrt{\dfrac{{{a}^{2}}}{{{\cos }^{2}}\theta }+\dfrac{{{b}^{2}}}{{{\sin }^{2}}\theta }} \\\ & Tt=\sqrt{\dfrac{{{a}^{2}}{{\sin }^{2}}\theta +{{b}^{2}}{{\cos }^{2}}\theta }{{{\cos }^{2}}\theta {{\sin }^{2}}\theta }} \\\ & Tt=\dfrac{\sqrt{{{a}^{2}}{{\sin }^{2}}\theta +{{b}^{2}}{{\cos }^{2}}\theta }}{\sin \theta \cos \theta }........................\left( 3 \right) \\\ \end{aligned}$$ Now we have from (2) and (3) we get $\begin{aligned} & P{{Y}_{1}}Tt=\dfrac{\sqrt{{{a}^{2}}{{\sin }^{2}}\theta +{{b}^{2}}{{\cos }^{2}}\theta }}{\sin \theta \cos \theta }\times \dfrac{\left( {{a}^{2}}-{{b}^{2}} \right)\sin \theta \cos \theta }{\sqrt{{{a}^{2}}{{\sin }^{2}}\theta +{{b}^{2}}{{\cos }^{2}}\theta }} \\\ & P{{Y}_{1}}Tt=\left( {{a}^{2}}-{{b}^{2}} \right) \\\ \end{aligned}$ Now consider equation (3). $$\begin{aligned} & T{{t}^{2}}=\dfrac{{{a}^{2}}{{\sin }^{2}}\theta +{{b}^{2}}{{\cos }^{2}}\theta }{{{\sin }^{2}}\theta {{\cos }^{2}}\theta } \\\ & T{{t}^{2}}={{a}^{2}}{{\sec }^{2}}\theta +{{b}^{2}}\cos e{{c}^{2}}\theta \\\ & T{{t}^{2}}={{a}^{2}}\left( 1+{{\tan }^{2}}\theta \right)+{{b}^{2}}\left( 1+{{\cot }^{2}}\theta \right) \\\ \end{aligned}$$ $T{{t}^{2}}={{a}^{2}}+{{b}^{2}}+{{a}^{2}}{{\tan }^{2}}\theta +{{b}^{2}}{{\cot }^{2}}\theta $ Now adding and subtracting 2ab we get $T{{t}^{2}}={{a}^{2}}+{{b}^{2}}+2ab+{{a}^{2}}{{\tan }^{2}}\theta +{{b}^{2}}{{\cot }^{2}}\theta -2ab$ Now we know that $\tan \theta \cot \theta =1$ hence we get $T{{t}^{2}}={{a}^{2}}+{{b}^{2}}+2ab+{{a}^{2}}{{\tan }^{2}}\theta +{{b}^{2}}{{\cot }^{2}}\theta -2ab{{\tan }^{2}}\theta {{\cot }^{2}}\theta $ Now we have ${{\left( a\pm b \right)}^{2}}={{a}^{2}}\pm 2ab+{{b}^{2}}$ hence we get $T{{t}^{2}}={{\left( a+b \right)}^{2}}+{{\left( a\tan \theta -b\cot \theta \right)}^{2}}$ Now we know that the minimum value of $\left( a\tan \theta -b\cot \theta \right)=0$ when $\tan \theta =\cot \theta $ . **Hence we have minimum value of $T{{t}^{2}}={{\left( a+b \right)}^{2}}$.** **Note:** Note to find ${{Y}_{1}}$ we can use the fact that ${{Y}_{1}}$ is nothing but foot of perpendicular on tangent from point (0, 0). Hence we get coordinates of ${{Y}_{1}}$ . Now since we have coordinates of P we can find the distance $P{{Y}_{1}}$ with distance formula.