Solveeit Logo
Login

Question

Question: If the tangent at \(\left( 1,1 \right)\) on \({{y}^{2}}=x{{\left( 2-x \right)}^{2}}\) meets the curv...

If the tangent at (1,1)\left( 1,1 \right) on y2=x(2−x)2{{y}^{2}}=x{{\left( 2-x \right)}^{2}} meets the curve again at P then find P.
A. (4,4)\left( 4,4 \right)
B. (−1,2)\left( -1,2 \right)
C. (94,38)\left( \dfrac{9}{4},\dfrac{3}{8} \right)
D. (1,2)\left( 1,2 \right)

Explanation

Solution

We first find the slope of the tangent at (1,1)\left( 1,1 \right) on y2=x(2−x)2{{y}^{2}}=x{{\left( 2-x \right)}^{2}}. We find the tangent and use the point P assuming variable of (m,n)\left( m,n \right) on both the tangent and the curve. We use the cubic equation to solve and find the solution of the problem.

Complete step-by-step solution:
We first find the tangent at (1,1)\left( 1,1 \right) on y2=x(2−x)2{{y}^{2}}=x{{\left( 2-x \right)}^{2}}. We find the differentiation of the curve which becomes the slope of the tangent.
Differentiating both sides of y2=x(2−x)2{{y}^{2}}=x{{\left( 2-x \right)}^{2}}.
\begin{aligned} & 2y\dfrac{dy}{dx}=x\left\\{ -2\left( 2-x \right) \right\\}+{{\left( 2-x \right)}^{2}}=\left( x-2 \right)\left( 2x+x-2 \right)=\left( x-2 \right)\left( 3x-2 \right) \\\ & \Rightarrow \dfrac{dy}{dx}=\dfrac{\left( x-2 \right)\left( 3x-2 \right)}{2y} \\\ \end{aligned}
Now if we are finding tangent of curve y=f(x)y=f\left( x \right) at point (a,b)\left( a,b \right) then the equation of tangent becomes (y−b)=[dydx](a,b)(x−a)\left( y-b \right)={{\left[ \dfrac{dy}{dx} \right]}_{\left( a,b \right)}}\left( x-a \right).
So, the tangent at (1,1)\left( 1,1 \right) on y2=x(2−x)2{{y}^{2}}=x{{\left( 2-x \right)}^{2}} will be (y−1)=[(x−2)(3x−2)2y](1,1)(x−1)\left( y-1 \right)={{\left[ \dfrac{\left( x-2 \right)\left( 3x-2 \right)}{2y} \right]}_{\left( 1,1 \right)}}\left( x-1 \right).
Simplifying the equation, we get the tangent’s equation as
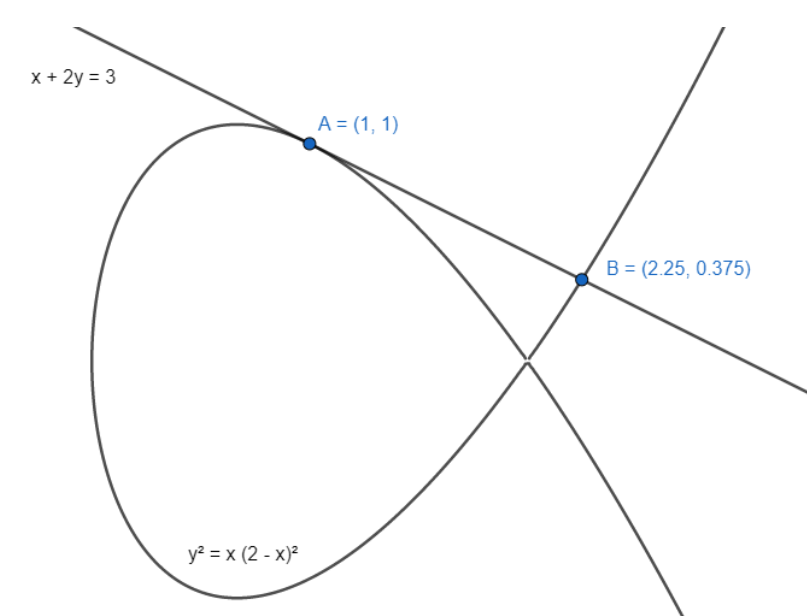
(y−1)=[(−1)(1)2](1,1)(x−1) ⇒2y−2=1−x ⇒x+2y=3 \begin{aligned} & \left( y-1 \right)={{\left[ \dfrac{\left( -1 \right)\left( 1 \right)}{2} \right]}_{\left( 1,1 \right)}}\left( x-1 \right) \\\ & \Rightarrow 2y-2=1-x \\\ & \Rightarrow x+2y=3 \\\ \end{aligned}

Now, the tangent meets the curve again at P other than the point (1,1)\left( 1,1 \right).
So, the intersection of the tangent x+2y=3x+2y=3 and curve y2=x(2−x)2{{y}^{2}}=x{{\left( 2-x \right)}^{2}} has two solutions, one of them being (1,1)\left( 1,1 \right) and the other one is point P.
Let the point P be (m,n)\left( m,n \right).
The point P resides on both the curve and the tangent.
Point P also satisfies x+2y=3x+2y=3 which means m+2n=3⇒m=3−2nm+2n=3\Rightarrow m=3-2n.
Point P is on the curve y2=x(2−x)2{{y}^{2}}=x{{\left( 2-x \right)}^{2}} which means n2=m(2−m)2{{n}^{2}}=m{{\left( 2-m \right)}^{2}}.
We put the value of m in the equation of n2=m(2−m)2{{n}^{2}}=m{{\left( 2-m \right)}^{2}}.
n2=m(2−m)2 ⇒n2=(3−2n)(2−(3−2n))2=(3−2n)(2n−1)2=−8n3+20n2−14n+3 ⇒8n3−19n2+14n−3=0 \begin{aligned} & {{n}^{2}}=m{{\left( 2-m \right)}^{2}} \\\ & \Rightarrow {{n}^{2}}=\left( 3-2n \right){{\left( 2-\left( 3-2n \right) \right)}^{2}}=\left( 3-2n \right){{\left( 2n-1 \right)}^{2}}=-8{{n}^{3}}+20{{n}^{2}}-14n+3 \\\ & \Rightarrow 8{{n}^{3}}-19{{n}^{2}}+14n-3=0 \\\ \end{aligned}
Now we solve the cubic equation of n using vanishing method.
8n3−19n2+14n−3=0 ⇒8(n−38)(n2−2n+1)=0 ⇒8(n−38)(n−1)2=0 \begin{aligned} & 8{{n}^{3}}-19{{n}^{2}}+14n-3=0 \\\ & \Rightarrow 8\left( n-\dfrac{3}{8} \right)\left( {{n}^{2}}-2n+1 \right)=0 \\\ & \Rightarrow 8\left( n-\dfrac{3}{8} \right){{\left( n-1 \right)}^{2}}=0 \\\ \end{aligned}
So, the value of n is n=1,38n=1,\dfrac{3}{8}.
Putting the value of n in the equation we get m=3−2(38)=3−34=94m=3-2\left( \dfrac{3}{8} \right)=3-\dfrac{3}{4}=\dfrac{9}{4}.
So, the other point is (m,n)≡(94,38)\left( m,n \right)\equiv \left( \dfrac{9}{4},\dfrac{3}{8} \right).
The correct option is C.

Note: We need to remember that the other point does not necessarily have to be the tangent of the curve at that point. So, we can’t use the formula of slope for the point. So, we have to solve the cubic equation after all. For solving the quadratic equation, we used the vanishing method. The process of finding roots in this method works by finding a point of x, say a for which the function y=f(x)y=f\left( x \right) becomes 0 which means y=f(a)=0y=f\left( a \right)=0 and (x−a)\left( x-a \right) becomes a root of the equation. In our problem we had 8n3−19n2+14n−3=08{{n}^{3}}-19{{n}^{2}}+14n-3=0. We knew we have a root as 1. So, y=f(1)=0y=f\left( 1 \right)=0. After we found that we put (x−1)\left( x-1 \right) as a root. The other way it can be done we use binary calculation and find the value 38\dfrac{3}{8} as the other root as y=f(38)=0y=f\left( \dfrac{3}{8} \right)=0. So, we take (x−38)\left( x-\dfrac{3}{8} \right) as a root of the polynomial and form factorisation.