Question

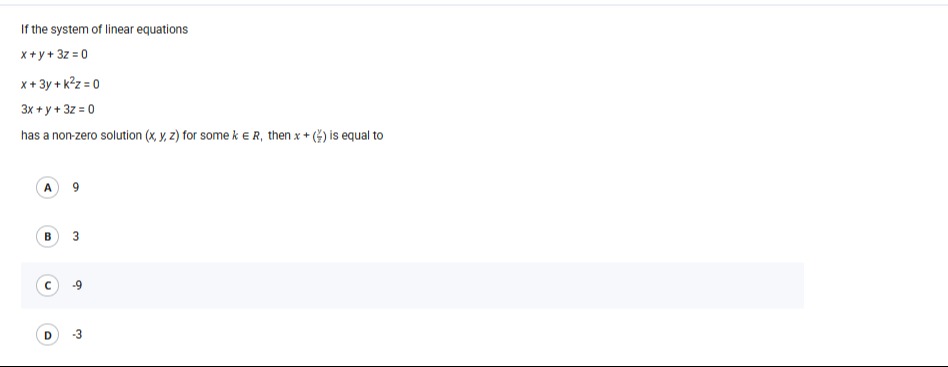
If the system of linear equations

$x+y+3z = 0$

$x + 3y + k^2z = 0$

$3x + y + 3z = 0$

has a non-zero solution $(x, y, z)$ for some $k \in R$, then $x + (\frac{y}{z})$ is equal to

• A. 9
• B. 3
• C. -9
• D. -3

Answer 1

Answer: (D)

-3

Answer 2

For a homogeneous system of linear equations to have a non-zero (non-trivial) solution, the determinant of its coefficient matrix must be zero.

The given system of equations is:

1. $x+y+3z = 0$
2. $x + 3y + k^2z = 0$
3. $3x + y + 3z = 0$

The coefficient matrix A is: $A = \begin{pmatrix} 1 & 1 & 3 \\ 1 & 3 & k^2 \\ 3 & 1 & 3 \end{pmatrix}$

For a non-zero solution, we must have $\det(A) = 0$. Let's calculate the determinant: $\det(A) = 1 \begin{vmatrix} 3 & k^2 \\ 1 & 3 \end{vmatrix} - 1 \begin{vmatrix} 1 & k^2 \\ 3 & 3 \end{vmatrix} + 3 \begin{vmatrix} 1 & 3 \\ 3 & 1 \end{vmatrix}$

$\det(A) = 1((3)(3) - (k^2)(1)) - 1((1)(3) - (k^2)(3)) + 3((1)(1) - (3)(3))$

$\det(A) = (9 - k^2) - (3 - 3k^2) + 3(1 - 9)$

$\det(A) = 9 - k^2 - 3 + 3k^2 + 3(-8)$

$\det(A) = 2k^2 + 6 - 24$

$\det(A) = 2k^2 - 18$

Set $\det(A) = 0$:

$2k^2 - 18 = 0$

$2k^2 = 18$

$k^2 = 9$

Now substitute $k^2 = 9$ back into the system of equations:

1. $x+y+3z = 0$
2. $x + 3y + 9z = 0$
3. $3x + y + 3z = 0$

We need to find the values of $x, y, z$ (or their ratios) that satisfy these equations. Consider equations (1) and (3): $x+y+3z = 0$ (1) $3x+y+3z = 0$ (3)

Subtract equation (1) from equation (3): $(3x+y+3z) - (x+y+3z) = 0 - 0$

$2x = 0$

$x = 0$

Now substitute $x=0$ into equation (1): $0+y+3z = 0$

$y = -3z$

Let's verify these values with equation (2) (substituting $x=0$ and $k^2=9$): $0 + 3y + 9z = 0$

$3y + 9z = 0$

$3y = -9z$

$y = -3z$

This is consistent with the result from equation (1).

Since the problem states there is a non-zero solution $(x, y, z)$, it means $(x, y, z) \neq (0,0,0)$. From $x=0$ and $y=-3z$, if $z=0$, then $y=0$ and $x=0$, which would give the trivial solution $(0,0,0)$. Therefore, $z$ must be non-zero. This ensures that $\frac{y}{z}$ is well-defined.

Finally, we need to calculate $x + (\frac{y}{z})$. Substitute the values we found: $x=0$ and $y=-3z$.

$x + \left(\frac{y}{z}\right) = 0 + \left(\frac{-3z}{z}\right)$

Since $z \neq 0$, we can cancel $z$:

$x + \left(\frac{y}{z}\right) = 0 + (-3)$

$x + \left(\frac{y}{z}\right) = -3$