Question

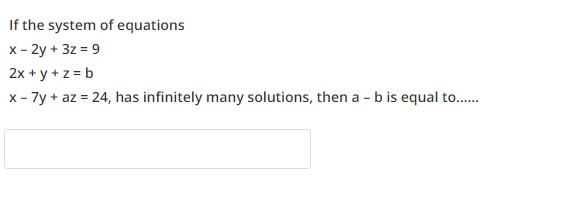
If the system of equations

$x - 2y + 3z = 9$

$2x + y + z = b$

$x-7y + az = 24$, has infinitely many solutions, then a – b is equal to……

Answer 1

5

Answer 2

The system of equations is given by:

1. $x - 2y + 3z = 9$

2. $2x + y + z = b$

3. $x - 7y + az = 24$

For a system of linear equations to have infinitely many solutions, two conditions must be met:

1. The determinant of the coefficient matrix must be zero.
2. The system must be consistent (which, for a $3 \times 3$ system with determinant 0, means the rank of the coefficient matrix is equal to the rank of the augmented matrix, and this rank is less than 3).

Let the coefficient matrix be $A$ and the augmented matrix be $[A|B]$.

$A = \begin{pmatrix} 1 & -2 & 3 \\ 2 & 1 & 1 \\ 1 & -7 & a \end{pmatrix}$, $B = \begin{pmatrix} 9 \\ b \\ 24 \end{pmatrix}$

Condition 1: $\det(A) = 0$.

$\det(A) = 1(1 \cdot a - 1 \cdot (-7)) - (-2)(2 \cdot a - 1 \cdot 1) + 3(2 \cdot (-7) - 1 \cdot 1)$

$\det(A) = 1(a + 7) + 2(2a - 1) + 3(-14 - 1)$

$\det(A) = a + 7 + 4a - 2 - 45$

$\det(A) = 5a - 40$

Setting $\det(A) = 0$, we get $5a - 40 = 0$, which implies $5a = 40$, so $a = 8$.

Now, with $a=8$, the system becomes:

1. $x - 2y + 3z = 9$

2. $2x + y + z = b$

3. $x - 7y + 8z = 24$

We can use row operations on the augmented matrix to find the condition for consistency.

$[A|B] = \begin{pmatrix} 1 & -2 & 3 & 9 \\ 2 & 1 & 1 & b \\ 1 & -7 & 8 & 24 \end{pmatrix}$

Apply $R_2 \to R_2 - 2R_1$ and $R_3 \to R_3 - R_1$:

$\begin{pmatrix} 1 & -2 & 3 & 9 \\ 0 & 5 & -5 & b - 18 \\ 0 & -5 & 5 & 15 \end{pmatrix}$

Apply $R_3 \to R_3 + R_2$:

$\begin{pmatrix} 1 & -2 & 3 & 9 \\ 0 & 5 & -5 & b - 18 \\ 0 & 0 & 0 & (b - 18) + 15 \end{pmatrix}$

$\begin{pmatrix} 1 & -2 & 3 & 9 \\ 0 & 5 & -5 & b - 18 \\ 0 & 0 & 0 & b - 3 \end{pmatrix}$

For infinitely many solutions, the rank of the coefficient matrix $\begin{pmatrix} 1 & -2 & 3 \\ 0 & 5 & -5 \\ 0 & 0 & 0 \end{pmatrix}$ (which is 2) must be equal to the rank of the augmented matrix $\begin{pmatrix} 1 & -2 & 3 & 9 \\ 0 & 5 & -5 & b - 18 \\ 0 & 0 & 0 & b - 3 \end{pmatrix}$.

This requires the last row of the augmented matrix to be entirely zero, which means the last entry in the last row must be zero.

$b - 3 = 0$, which implies $b = 3$.

Thus, for the system to have infinitely many solutions, we must have $a=8$ and $b=3$.

The question asks for the value of $a - b$.

$a - b = 8 - 3 = 5$.