Question

If the sum of the lengths of the hypotenuse and a side of a right triangle is given, show that the area of the triangle is maximum when the angle of between them is $\dfrac{\pi }{3}.$

Answer 1

Hint: For solving this question, first let the length of the hypotenuse of the right triangle be ‘x’ and the height of the right angle be ‘y’. By using the Pythagoras theorem, we find the base of the right-angle triangle and then the area of a triangle. By using this methodology, we get the value of x and y and proved that the area of the triangle is maximum when the angle of between them is $\dfrac{\pi }{3}.$

Complete step-by-step soltuion -
__
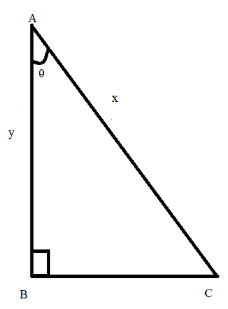
Let, the height of the hypotenuse of the right-angle triangle be ‘x’ and the height of the right-angle triangle be ‘y’.
By applying the Pythagoras theorem which can be stated as: ${{h}^{2}}={{b}^{2}}+{{p}^{2}}$
On putting h = x and p = y,
The base of the right-angled triangle is:
$\begin{aligned} & {{x}^{2}}={{b}^{2}}+{{y}^{2}} \\\ & {{b}^{2}}={{x}^{2}}-{{y}^{2}} \\\ & \therefore b=\sqrt{{{x}^{2}}-{{y}^{2}}} \\\ \end{aligned}$
Then, the area of the triangle $=\dfrac{1}{2}\times base\times height$
Area of the triangle $=\dfrac{1}{2}\times \sqrt{{{x}^{2}}-{{y}^{2}}}\times y$
But it is given,
$\begin{aligned} & x+y=p \\\ & \therefore x=p-y \\\ \end{aligned}$
Putting the value of x in the area of the right-angle triangle,
$\begin{aligned} & \text{Area}=\dfrac{1}{2}\times \sqrt{{{\left( p-y \right)}^{2}}-{{y}^{2}}}\times y \\\ & \text{Area}=\dfrac{1}{2}\times y\sqrt{{{p}^{2}}+{{y}^{2}}-2py-{{y}^{2}}} \\\ & \text{Area}=\dfrac{1}{2}\times y\times \sqrt{{{p}^{2}}-2py} \\\ \end{aligned}$
Squaring both the sides, we get:
$\begin{aligned} & {{\left( \text{Area} \right)}^{2}}=\dfrac{1}{4}\times {{y}^{2}}\times \left( {{p}^{2}}-2py \right) \\\ & {A}'=\dfrac{1}{4}\times {{y}^{2}}\times \left( {{p}^{2}}-2py \right) \\\ & {A}'=\dfrac{1}{4}{{p}^{2}}{{y}^{2}}-\dfrac{1}{2}p{{y}^{3}} \\\ \end{aligned}$
For maximum area and minimum area,
$\begin{aligned} & \dfrac{d{A}'}{dy}=0 \\\ & \dfrac{d{A}'}{dy}=\dfrac{1}{4}\times 2{{p}^{2}}y-\dfrac{1}{2}\times 3p{{y}^{2}} \\\ & \dfrac{d{A}'}{dy}=\dfrac{1}{2}{{p}^{2}}y-\dfrac{3}{2}p{{y}^{2}} \\\ & \dfrac{1}{2}{{p}^{2}}y=\dfrac{3}{2}p{{y}^{2}} \\\ & y=\dfrac{p}{3} \\\ & x=p-y \\\ & x=p-\dfrac{p}{3}=\dfrac{2p}{3} \\\ \end{aligned}$
For checking the area maximum,
$\begin{aligned} & \dfrac{{{d}^{2}}{A}'}{d{{y}^{2}}}=\dfrac{d}{dy}\left( \dfrac{1}{4}\times 2{{p}^{2}}y-\dfrac{1}{2}\times 3p{{y}^{2}} \right) \\\ & \dfrac{{{d}^{2}}{A}'}{d{{y}^{2}}}=\dfrac{1}{2}{{p}^{2}}-\dfrac{1}{2}\times 3p\times 2y \\\ & \dfrac{{{d}^{2}}{A}'}{d{{y}^{2}}}=\dfrac{1}{2}{{p}^{2}}-3py \\\ \end{aligned}$
Putting $y=\dfrac{p}{3}$, we get
$\begin{aligned} & \dfrac{{{d}^{2}}{A}'}{d{{y}^{2}}}=\dfrac{1}{2}{{p}^{2}}-3py \\\ & \Rightarrow \dfrac{1}{2}{{p}^{2}}-3p\left( \dfrac{p}{3} \right) \\\ & \Rightarrow \dfrac{1}{2}{{p}^{2}}-{{p}^{2}} \\\ & \Rightarrow -\dfrac{1}{2}{{p}^{2}} \\\ & \therefore \dfrac{{{d}^{2}}{A}'}{d{{y}^{2}}}<0 \\\ \end{aligned}$
Here, the area of the triangle is maximum when
$x=\dfrac{2p}{3}\text{ and }y=\dfrac{p}{3}$
Cosine of the right-angle triangle is the ratio of base to hypotenuse. In our figure, hypotenuse = x and base = y, so
$\begin{aligned} & \cos \theta =\dfrac{y}{x} \\\ & \cos \theta =\dfrac{\dfrac{p}{3}}{2\times \dfrac{p}{3}} \\\ & \cos \theta =\dfrac{1}{2} \\\ \end{aligned}$
Therefore, the value of $\cos \theta$ is $\dfrac{1}{2}$, when $\theta =\dfrac{\pi }{3}$.
Hence, the area is maximum if the angle between the hypotenuse and the side is $\dfrac{\pi }{3}$.

Note: Students must be careful while applying the condition for maximum area. They must use the concept of the second derivative to prove that the area is maximum at the particular value of y. This is the key step and it should not be avoided as most people avoid the second derivative and proceed after the result obtained in the first derivative only.