Question

If the sum of lengths of the hypotenuse and a side of a right angled triangle is given, show that the area of the triangle is maximum, when the angle between is $\dfrac{\pi }{3}$.

Answer 1

Hint: We will use the concept of Pythagoras theorem and we will apply the formula $\text{area of triangle = }\dfrac{1}{2}\times g\times f$ , where g is base and f is height, to solve the question further. Also we will use differentiation till the second derivative for the maximum and minimum values. Moreover, with the help of the formula that $\cos \left( \alpha \right)=\dfrac{\text{base}}{\text{hypotenuse}}$ we will find the value of the angle $\alpha$ and find the maximum value of the angle for which the area of the triangle is maximum.

Complete step-by-step answer:

Let us consider the diagram for the question as shown below.

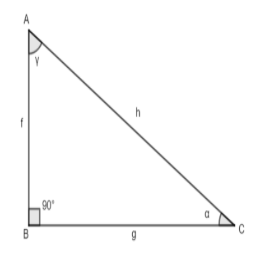
Now, according to the question we have the sum of lengths of the hypotenuse and a side of a right angled triangle is given to us. But since it is not equal to anything right now, so, we will consider that this sum is equal to a. Numerically, we can write it as g + h = a or h = a – g.
Now, we will use the Pythagoras theorem. Therefore, by the Pythagoras theorem we have ${{\left( AC \right)}^{2}}={{\left( AB \right)}^{2}}+{{\left( BC \right)}^{2}}$. As, we have AC = h, AB = f and BC = g. Thus, by substituting these values into the Pythagoras equation we will get,
$\begin{aligned} & {{\left( AC \right)}^{2}}={{\left( AB \right)}^{2}}+{{\left( BC \right)}^{2}} \\\ & \Rightarrow {{h}^{2}}={{f}^{2}}+{{g}^{2}} \\\ & \Rightarrow {{f}^{2}}={{h}^{2}}-{{g}^{2}} \\\ & \Rightarrow f=\sqrt{{{h}^{2}}-{{g}^{2}}} \\\ \end{aligned}$
Now, as we are supposed to show that the area of the triangle is maximum. So, for that we will first find the area of the triangle. This can be carried out by the formula $\text{area of triangle = }\dfrac{1}{2}\times \text{base}\times \text{height}$. Therefore, we get $\text{area of triangle = }\dfrac{1}{2}\times g\times f$. After substituting the value of g by above we will get,
$\begin{aligned} & \text{area of triangle = }\dfrac{1}{2}\times \sqrt{{{h}^{2}}-{{g}^{2}}}\times g \\\ & \Rightarrow \text{area of triangle = }\dfrac{1}{2}\times \sqrt{{{\left( a-g \right)}^{2}}-{{g}^{2}}}\times g\,\,\,\,\left[ \because h=a-g \right] \\\ & \Rightarrow \text{area of triangle = }\dfrac{1}{2}\times \sqrt{{{a}^{2}}+{{g}^{2}}-2ag-{{g}^{2}}}\times g\,\,\,\,\left[ \because {{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab \right] \\\ & \Rightarrow \text{area of triangle = }\dfrac{1}{2}\times \sqrt{{{a}^{2}}-2ag}\times g \\\ \end{aligned}$
After squaring both the sides we will get,
$\begin{aligned} & {{\left( \text{area of triangle} \right)}^{2}}\text{= }{{\left( \dfrac{1}{2}\times \sqrt{{{a}^{2}}-2ag}\times g \right)}^{2}} \\\ & \Rightarrow {{\left( \text{area of triangle} \right)}^{2}}\text{= }\dfrac{1}{4}\times \left( {{a}^{2}}-2ag \right)\times {{g}^{2}} \\\ & \Rightarrow {{\left( \text{area of triangle} \right)}^{2}}\text{= }\dfrac{{{g}^{2}}}{4}\times \left( {{a}^{2}}-2ag \right) \\\ \end{aligned}$
Using differentiation with respect to g will result into $\begin{aligned} & \dfrac{d}{dg}\left[ {{\left( \text{area of triangle} \right)}^{2}} \right]\text{= }\dfrac{d}{dg}\left[ \dfrac{{{g}^{2}}}{4}\times \left( {{a}^{2}}-2ag \right) \right] \\\ & \Rightarrow \dfrac{d}{dg}\left[ {{\left( \text{area of triangle} \right)}^{2}} \right]\text{= }\left( {{a}^{2}}-2ag \right)\dfrac{d}{dg}\left( \dfrac{{{g}^{2}}}{4} \right)+\dfrac{{{g}^{2}}}{4}\dfrac{d}{dg}\left( {{a}^{2}}-2ag \right)\,\,\,\,\left[ \because \dfrac{d}{dx}\left( uv \right)=v\dfrac{d}{dx}\left( u \right)+u\dfrac{d}{dx}\left( v \right) \right] \\\ & \Rightarrow \dfrac{d}{dg}\left[ {{\left( \text{area of triangle} \right)}^{2}} \right]\text{= }\left( {{a}^{2}}-2ag \right)\dfrac{1}{4}\left( 2g \right)+\dfrac{{{g}^{2}}}{4}\left( -2a \right) \\\ & \Rightarrow \dfrac{d}{dg}\left[ {{\left( \text{area of triangle} \right)}^{2}} \right]\text{= }\left( {{a}^{2}}-2ag \right)\dfrac{g}{2}-\dfrac{a{{g}^{2}}}{2} \\\ & \Rightarrow \dfrac{d}{dg}\left[ {{\left( \text{area of triangle} \right)}^{2}} \right]\text{= }\dfrac{{{a}^{2}}g}{2}-a{{g}^{2}}-\dfrac{a{{g}^{2}}}{2} \\\ & \Rightarrow \dfrac{d}{dg}\left[ {{\left( \text{area of triangle} \right)}^{2}} \right]\text{= }\dfrac{{{a}^{2}}g}{2}-3\dfrac{a{{g}^{2}}}{2} \\\ \end{aligned}$
Now, in order to find the maximum area of the triangle, first we will equate the first derivative to 0. Thus we get,
$\begin{aligned} & \dfrac{d}{dg}\left[ {{\left( \text{area of triangle} \right)}^{2}} \right]\text{= 0} \\\ & \Rightarrow \dfrac{{{a}^{2}}g}{2}-3\dfrac{a{{g}^{2}}}{2}=0 \\\ & \Rightarrow {{a}^{2}}g-3a{{g}^{2}}=0 \\\ \end{aligned}$
Taking ‘ag’ as a common term in the equation after which it results into ag(a – 3g) = 0. Therefore, we get ag = 0 or a – 3g = 0. This further gives the value of g = 0 or g = $\dfrac{a}{3}$. So, we have got a critical value. Now, we will first find the second derivative of the area of the triangle and then we will substitute this value to find its maximum and minimum values. So, the second derivative by differentiating $\dfrac{d}{dg}\left[ {{\left( \text{area of triangle} \right)}^{2}} \right]\text{= }\dfrac{{{a}^{2}}g}{2}-3\dfrac{a{{g}^{2}}}{2}$ with respect to g, we get
$\begin{aligned} & \dfrac{d}{dg}\left[ \dfrac{d}{dg}\left[ {{\left( \text{area of triangle} \right)}^{2}} \right] \right]\text{= }\dfrac{d}{dg}\left[ \dfrac{{{a}^{2}}g}{2}-3\dfrac{a{{g}^{2}}}{2} \right] \\\ & \Rightarrow \dfrac{{{d}^{2}}}{d{{g}^{2}}}\left[ {{\left( \text{area of triangle} \right)}^{2}} \right]\text{= }\dfrac{d}{dg}\left( \dfrac{{{a}^{2}}g}{2} \right)-\dfrac{d}{dg}\left( 3\dfrac{a{{g}^{2}}}{2} \right) \\\ & \Rightarrow \dfrac{{{d}^{2}}}{d{{g}^{2}}}\left[ {{\left( \text{area of triangle} \right)}^{2}} \right]\text{= }\left( \dfrac{{{a}^{2}}}{2} \right)\dfrac{d}{dg}\left( g \right)-\left( \dfrac{3a}{2} \right)\dfrac{d}{dg}\left( {{g}^{2}} \right) \\\ & \Rightarrow \dfrac{{{d}^{2}}}{d{{g}^{2}}}\left[ {{\left( \text{area of triangle} \right)}^{2}} \right]\text{= }\left( \dfrac{{{a}^{2}}}{2} \right)-\left( \dfrac{3a}{2} \right)\left( 2g \right)\,\,\,\,\left[ \because \dfrac{dg}{dg}=1,\dfrac{d\left( {{g}^{2}} \right)}{dg}=2g\dfrac{dg}{dg} \right] \\\ & \Rightarrow \dfrac{{{d}^{2}}}{d{{g}^{2}}}\left[ {{\left( \text{area of triangle} \right)}^{2}} \right]\text{= }\dfrac{{{a}^{2}}}{2}-3ag \\\ \end{aligned}$
Now, we will substitute the value of g in equation $\dfrac{{{d}^{2}}}{d{{g}^{2}}}\left[ {{\left( \text{area of triangle} \right)}^{2}} \right]\text{= }\dfrac{{{a}^{2}}}{2}-3ag$. Thus, we get
$\begin{aligned} & \dfrac{{{d}^{2}}}{d{{g}^{2}}}\left[ {{\left( \text{area of triangle} \right)}^{2}} \right]\text{= }\dfrac{{{a}^{2}}}{2}-3ag \\\ & \Rightarrow \dfrac{{{d}^{2}}}{d{{g}^{2}}}\left[ {{\left( \text{area of triangle} \right)}^{2}} \right]\text{= }\dfrac{{{a}^{2}}}{2}-3a\left( \dfrac{a}{3} \right) \\\ & \Rightarrow \dfrac{{{d}^{2}}}{d{{g}^{2}}}\left[ {{\left( \text{area of triangle} \right)}^{2}} \right]\text{= }\dfrac{{{a}^{2}}}{2}-{{a}^{2}} \\\ & \Rightarrow \dfrac{{{d}^{2}}}{d{{g}^{2}}}\left[ {{\left( \text{area of triangle} \right)}^{2}} \right]\text{= }\dfrac{{{a}^{2}}-2{{a}^{2}}}{2} \\\ & \Rightarrow \dfrac{{{d}^{2}}}{d{{g}^{2}}}\left[ {{\left( \text{area of triangle} \right)}^{2}} \right]\text{= }-\dfrac{{{a}^{2}}}{2} \\\ \end{aligned}$
Clearly the value is less than 0. So, the second derivative is maximum at this value. Therefore we now have $g=\dfrac{a}{3},h=\dfrac{2a}{3}$. As we know that $\cos \left( \alpha \right)=\dfrac{\text{base}}{\text{hypotenuse}}$ so, by substituting the values of g as a base and h as hypotenuse we will get $\cos \left( \alpha \right)=\dfrac{g}{h}$ and by putting the values in this equation further results into
$\begin{aligned} & \cos \left( \alpha \right)=\dfrac{\dfrac{a}{3}}{\dfrac{2a}{3}} \\\ & \Rightarrow \cos \left( \alpha \right)=\dfrac{3a}{2\left( 3 \right)a} \\\ & \Rightarrow \cos \left( \alpha \right)=\dfrac{1}{2} \\\ \end{aligned}$
As we know that $\cos \left( \dfrac{\pi }{3} \right)=\dfrac{1}{2}$ thus we get $\cos \left( \alpha \right)=\cos \left( \dfrac{\pi }{3} \right)$. Now we will use the formula given by $\cos \left( x \right)=\cos \left( y \right)$ resulting into $x=n\pi \pm y$ will give us $\alpha =n\pi \pm \dfrac{\pi }{3}$ where n are integers. As n = 0 we will have $\alpha =\dfrac{\pi }{3}$.
Hence, the area of the triangle is maximum, when the angle between is $\dfrac{\pi }{3}$.

Note: It should be noted that the sum that is given in the question is between the hypotenuse and the base of the triangle as we are considering angle $\alpha$ here. But if we take the sum of the hypotenuse and the side AB then the angle is to be considered is $\gamma$ only. If this point is not followed then the answer will be wrong. We can also use the formula $\sin \left( \alpha \right)=\dfrac{\text{perpendicular}}{\text{hypotenuse}}$ and solve the question further. This will also give the right answer.