Question

If the sum of all the roots of the equation $e^{2x} - 11e^x - 45e^{-x} + 81/2 = 0$ is $log_e p$, then p is equal to _.

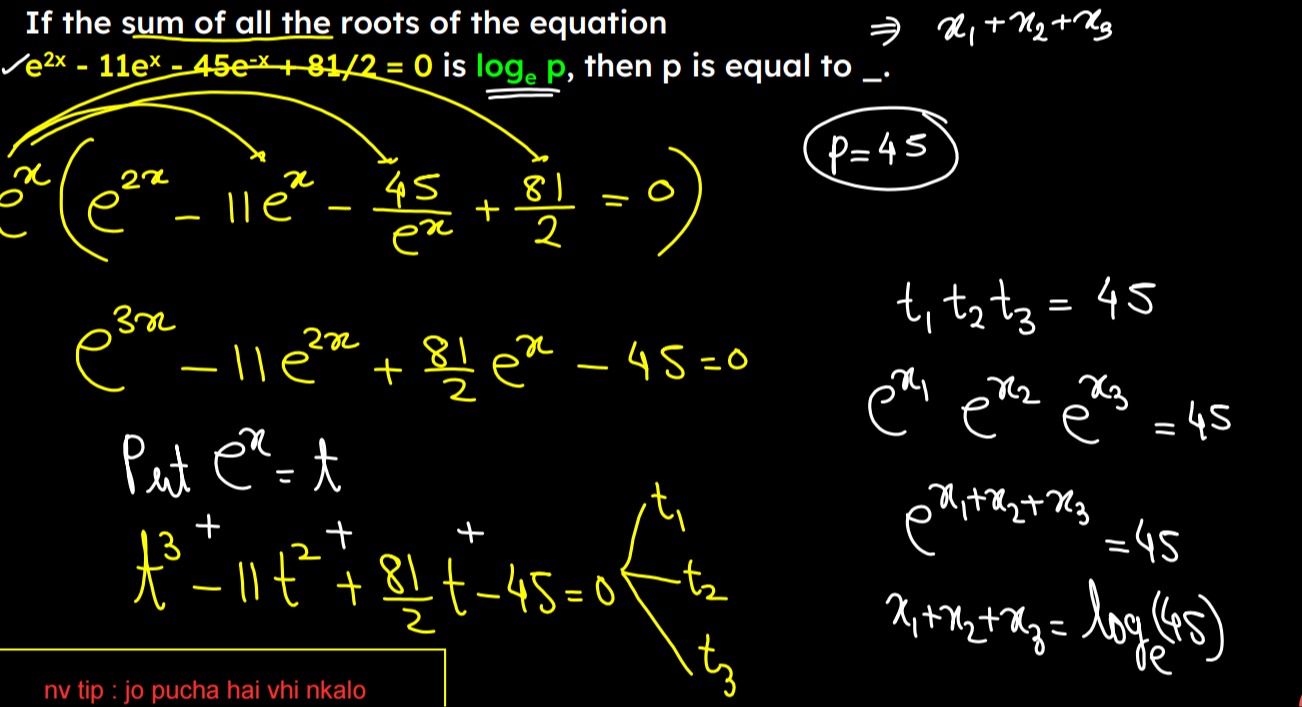
• A. 45
• B. 81/2
• C. 11
• D. 9/2

Answer 1

Answer: (A)

45

Answer 2

The given equation is $e^{2x} - 11e^x - 45e^{-x} + 81/2 = 0$. Multiplying the equation by $e^x$ to eliminate the negative exponent, we get: $e^x(e^{2x}) - e^x(11e^x) - e^x(45e^{-x}) + e^x(81/2) = 0$ $e^{3x} - 11e^{2x} - 45 + \frac{81}{2}e^x = 0$ Rearranging the terms, we have: $e^{3x} - 11e^{2x} + \frac{81}{2}e^x - 45 = 0$ Let $t = e^x$. Substituting $t$ into the equation gives a cubic polynomial in $t$: $t^3 - 11t^2 + \frac{81}{2}t - 45 = 0$ Let the roots of this cubic equation be $t_1, t_2, t_3$. If $x_1, x_2, x_3$ are the roots of the original exponential equation, then $t_1 = e^{x_1}$, $t_2 = e^{x_2}$, and $t_3 = e^{x_3}$. According to Vieta's formulas, for a cubic equation $at^3 + bt^2 + ct + d = 0$, the product of the roots is $t_1 t_2 t_3 = -d/a$. In our equation, $a=1$, $b=-11$, $c=81/2$, and $d=-45$. So, the product of the roots is $t_1 t_2 t_3 = -(-45)/1 = 45$. Substituting back $t_i = e^{x_i}$, we get: $e^{x_1} \cdot e^{x_2} \cdot e^{x_3} = 45$ $e^{x_1+x_2+x_3} = 45$ The problem states that the sum of all the roots of the given equation is $log_e p$. So, $x_1+x_2+x_3 = log_e p$. Taking the natural logarithm of both sides of $e^{x_1+x_2+x_3} = 45$: $log_e(e^{x_1+x_2+x_3}) = log_e 45$ $x_1+x_2+x_3 = log_e 45$ Comparing this with $x_1+x_2+x_3 = log_e p$, we find that $p = 45$.