Question

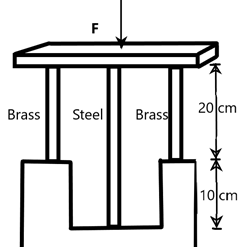
If the stress in the steel rod is ‘x’ then the value of $\dfrac{x}{5}$ is (in MPa)? Given the area of the cross section of all the rods as $1\times {{10}^{-4}}{{m}^{2}}$ and the total force acting on the system as 5000N. Also, ${{Y}_{steel}}=2\times {{10}^{11}}N{{m}^{-2}}\text{ and }{{Y}_{brass}}=1\times {{10}^{11}}N{{m}^{-2}}$.

Answer 1

We need to understand the relation between the stress and the given parameters such as the Young’s modulus, area of cross section of the rods and the force acting on the rods to find the required solution to this problem easily.

Complete answer:
We are given a system of three rods placed in a particular arrangement such that a force acting on the plane above them as we can see in the figure is equally applied to each of them.
We know that a perpendicular force acting on a rod can cause a longitudinal compression or expansion for the rod which is defined as its longitudinal strain. We have derived the formula for the Young’s modulus as the ratio between the longitudinal stress to the longitudinal strain from which we can get the strain related to the force applied as –

& Y=\dfrac{Stress}{Strain} \\\ & \Rightarrow Y=\dfrac{\dfrac{F}{A}}{\dfrac{\Delta l}{l}} \\\ & \Rightarrow Y=\dfrac{Fl}{A\Delta l} \\\ & \therefore \Delta l=\dfrac{Fl}{YA} \\\ \end{aligned}$$ We know that the strain experienced by all three of the rods should be the same. So, we can calculate the force experienced by each of them as – $$\begin{aligned} & \Delta l=\dfrac{Fl}{YA} \\\ & \therefore F=\dfrac{\Delta lYA}{l} \\\ \end{aligned}$$  Now, we can write the total force on the plane as the sum of the force acting on each of the rods as – $$\begin{aligned} & F={{F}_{B}}+{{F}_{S}}+{{F}_{B}} \\\ & \Rightarrow 5000N=\dfrac{\Delta l{{Y}_{B}}{{A}_{B}}}{{{l}_{B}}}+\dfrac{\Delta l{{Y}_{S}}{{A}_{S}}}{{{l}_{B}}}+\dfrac{\Delta l{{Y}_{B}}{{A}_{B}}}{{{l}_{B}}} \\\ & \Rightarrow 5000=\dfrac{\Delta l(1\times {{10}^{11}})(1\times {{10}^{-4}})}{0.2}+\dfrac{\Delta l(2\times {{10}^{11}})(1\times {{10}^{-4}})}{0.3}+\dfrac{\Delta l(1\times {{10}^{11}})(1\times {{10}^{-4}})}{0.2} \\\ & \Rightarrow 5000=(5\times {{10}^{7}})\Delta l+(6.67\times {{10}^{7}})\Delta l+(5\times {{10}^{7}})\Delta l \\\ & \Rightarrow 5000=(16.67\times {{10}^{7}})\Delta l \\\ & \Rightarrow \Delta l=\dfrac{5000}{16.67\times {{10}^{7}}} \\\ & \therefore \Delta l=2.99\times {{10}^{-5}}m=0.03mm \\\ \end{aligned}$$ Now, we can find the stress involved in the steel rod by using all the given information as – $$\begin{aligned} & \Delta l=\dfrac{{{F}_{S}}{{l}_{S}}}{{{Y}_{S}}{{A}_{S}}} \\\ & \Rightarrow \dfrac{\Delta l}{{{l}_{S}}}=\dfrac{{{F}_{S}}}{{{Y}_{S}}{{A}_{S}}} \\\ \end{aligned}$$ $$\begin{aligned} & \text{but,} \\\ & Stress,x=\dfrac{{{F}_{S}}}{{{A}_{S}}} \\\ & \Rightarrow x={{Y}_{S}}\dfrac{\Delta l}{{{l}_{S}}} \\\ & \Rightarrow x=(2\times {{10}^{11}})\dfrac{0.03\times {{10}^{-3}}}{0.3} \\\ & \therefore x=2\times {{10}^{7}}Pa=20MPa \\\ \end{aligned}$$ So, the stress on the steel rod ‘x’ is 20 MPa. We are asked to find $$\dfrac{x}{5}$$. $$\begin{aligned} & x=20MPa \\\ & \therefore \dfrac{x}{5}=4MPa \\\ \end{aligned}$$ This is the required solution. **Note:** The Young’s modulus is the ratio between the longitudinal stress to the longitudinal strain. It is independent of the dimensions of the object on which a perpendicular force is acting, it is a characteristic property of the material of the object.