Question

If the straight line $x\cos \alpha + y\sin \alpha = p$ touches the ellipse $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$ , prove that ${p^2} = {a^2}{\cos ^2}\alpha + {b^2}{\sin ^2}\alpha$.

Answer 1

Here, in the given question, a straight line touches the ellipse. And we are asked to prove a relation given on the basis of equations of line and ellipse. We will use the fact that at a point of intersection, the slope of the straight line and tangent to ellipse must be equal to each other and prove the given relation.

Complete step-by-step solution:
Given, Equation of straight line $x\cos \alpha + y\sin \alpha = p$, and,
Equation of the curve (ellipse) is $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$
Or we can write it as, ${b^2}{x^2} + {a^2}{y^2} = {a^2}{b^2}$
Let this straight line and ellipse intersect each other at point $P\left( {{x_1},{y_1}} \right)$

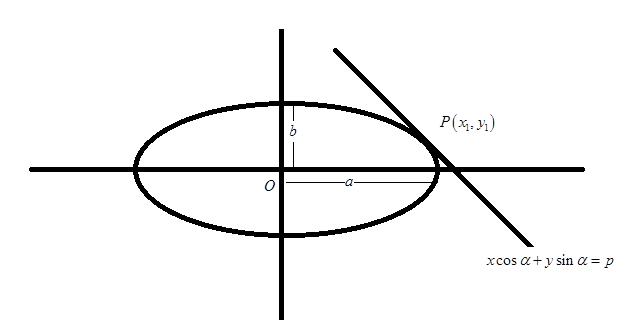
Therefore, $P\left( {{x_1},{y_1}} \right)$ must satisfy the equation of line as well as ellipse.
${x_1}\cos \alpha + {y_1}\sin \alpha = p$
And ${b^2}x_1^2 + {a^2}y_1^2 = {a^2}{b^2}$
Now, slope of the straight line is $- \dfrac{{\cos \alpha }}{{\sin \alpha }}$
Slope of the tangent to the ellipse at point $P\left( {{x_1},{y_1}} \right)$ is ${\left( {\dfrac{{dy}}{{dx}}} \right)_{\left( {{x_1},{y_1}} \right)}}$.
Differentiating ${b^2}{x^2} + {a^2}{y^2} = {a^2}{b^2}$, w.r.t. $x$, we get

$$2{b^2}x + 2{a^2}y\dfrac{{dy}}{{dx}} = 0 \\\ \Rightarrow \dfrac{{dy}}{{dx}} = - \dfrac{{{b^2}x}}{{{a^2}y}} \\\ \Rightarrow {\left( {\dfrac{{dy}}{{dx}}} \right)_{\left( {{x_1},{y_1}} \right)}} = - \dfrac{{{b^2}{x_1}}}{{{a^2}{y_1}}} \\\$$

According to the question, at point $P\left( {{x_1},{y_1}} \right)$, The slope of the straight line and the tangent to the ellipse must be equal to each other.

$$\therefore - \dfrac{{{b^2}{x_1}}}{{{a^2}{y_1}}} = - \dfrac{{\cos \alpha }}{{\sin \alpha }} \\\ \Rightarrow \dfrac{{{x_1}}}{{{a^2}\cos \alpha }} = \dfrac{{{y_1}}}{{{b^2}\sin \alpha }} = \lambda \left( {say} \right) \\\$$

$\Rightarrow {x_1} = \lambda {a^2}\;\cos \alpha$ and ${y_1} = \lambda {b^2}\sin \alpha$
Putting these values in the equation of line at $P\left( {{x_1},{y_1}} \right)$ , we get

$$\lambda {a^2}\;{\cos ^2}\alpha + \lambda {b^2}{\sin ^2}\alpha = p \\\ \Rightarrow \lambda = \dfrac{p}{{{a^2}{{\cos }^2}\alpha + {b^2}{{\sin }^2}\alpha }} \\\$$

Therefore, the values for ${x_1}$and ${y_1}$are
${x_1} = \dfrac{{p{a^2}\;{{\cos }^2}\alpha }}{{{a^2}{{\cos }^2}\alpha + {b^2}{{\sin }^2}\alpha }}$ and ${y_1} = \dfrac{{p{b^2}\;{{\sin }^2}\alpha }}{{{a^2}{{\cos }^2}\alpha + {b^2}{{\sin }^2}\alpha }}$
Putting these values in the equation of the ellipse at point $P\left( {{x_1},{y_1}} \right)$, we get

$$\dfrac{{{b^2}{p^2}{a^4}\;{{\cos }^2}\alpha }}{{{{\left( {{a^2}{{\cos }^2}\alpha + {b^2}{{\sin }^2}\alpha } \right)}^2}}} + \dfrac{{{b^4}{p^2}{a^2}\;{{\sin }^2}\alpha }}{{{{\left( {{a^2}{{\cos }^2}\alpha + {b^2}{{\sin }^2}\alpha } \right)}^2}}} = {a^2}{b^2} \\\ \Rightarrow \dfrac{{{b^2}{p^2}{a^2}\left( {{a^2}{{\cos }^2}\alpha + {b^2}{{\sin }^2}\alpha } \right)}}{{{{\left( {{a^2}{{\cos }^2}\alpha + {b^2}{{\sin }^2}\alpha } \right)}^2}}} = {a^2}{b^2} \\\ \Rightarrow \dfrac{{{p^2}}}{{\left( {{a^2}{{\cos }^2}\alpha + {b^2}{{\sin }^2}\alpha } \right)}} = 1 \\\ \Rightarrow {p^2} = {a^2}{\cos ^2}\alpha + {b^2}{\sin ^2}\alpha \\\$$

Note: Whenever we face such types of questions, one thing to keep in mind is that at the point of intersection of two curves, their slopes must be equal to each other. So, firstly find out the equation of both the curves at general point $P\left( {{x_1},{y_1}} \right)$. And Slope of the tangent to the ellipse at point $P\left( {{x_1},{y_1}} \right)$ is ${\left( {\dfrac{{dy}}{{dx}}} \right)_{\left( {{x_1},{y_1}} \right)}}$.