Question

If the sound heard by observer, whose equation is given as $y=8\sin10\pi t \cos200\pi t$ at $x=0$, then number of beat frequency heard by observer is $2k$. Then the value of $k$ is

Answer 1

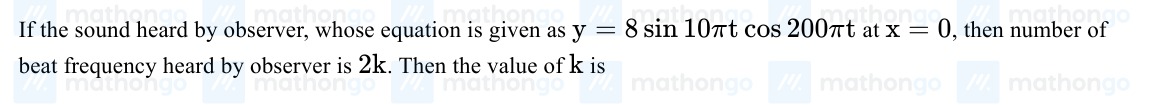
5

Answer 2

The given equation of the sound wave at $x=0$ is $y=8\sin10\pi t \cos200\pi t$. This equation represents the superposition of two simple harmonic waves. We can use the trigonometric product-to-sum identity $2 \sin A \cos B = \sin(A+B) + \sin(A-B)$ to rewrite the equation.

Let $A = 10\pi t$ and $B = 200\pi t$. The equation can be written as: $y = 4 \times (2 \sin(10\pi t) \cos(200\pi t))$ Using the identity, $2 \sin(10\pi t) \cos(200\pi t) = \sin(10\pi t + 200\pi t) + \sin(10\pi t - 200\pi t)$. $y = 4 \times (\sin(210\pi t) + \sin(-190\pi t))$ Since $\sin(-\theta) = -\sin(\theta)$, we have: $y = 4 \times (\sin(210\pi t) - \sin(190\pi t))$ $y = 4 \sin(210\pi t) - 4 \sin(190\pi t)$

This equation shows the superposition of two waves with angular frequencies $\omega_1 = 210\pi$ and $\omega_2 = 190\pi$. The frequency of a wave is given by $f = \omega / (2\pi)$. The frequencies of the two waves are: $f_1 = \frac{\omega_1}{2\pi} = \frac{210\pi}{2\pi} = 105$ Hz $f_2 = \frac{\omega_2}{2\pi} = \frac{190\pi}{2\pi} = 95$ Hz

When two sound waves of slightly different frequencies $f_1$ and $f_2$ are heard simultaneously, beats are produced. The beat frequency is the absolute difference between the two frequencies: Beat frequency $= |f_1 - f_2|$ Beat frequency $= |105 \text{ Hz} - 95 \text{ Hz}| = 10 \text{ Hz}$.

The problem states that the number of beat frequency heard by the observer is $2k$. So, we have: $10 = 2k$

To find the value of $k$, we divide both sides by 2: $k = \frac{10}{2}$ $k = 5$