Question

If the slope of the line passing through the points (2, 5) and (x, 3) is 2, find the value of x.

Answer 1

Hint: We know that slope of a line joining two points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is equal to the tangent of the angle made by the line with x-axis in anticlockwise direction given by as follows:
$slope=\tan \theta =\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$
Complete step-by-step answer:
We have been given the slope of a line joining the points (x, 3) and (2, 5) is 2.
We know that the slope of a line joining two points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is equal to the tangent of the angle made by the line with x-axis in anticlockwise direction given by as follows:
$slope=\tan \theta =\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$

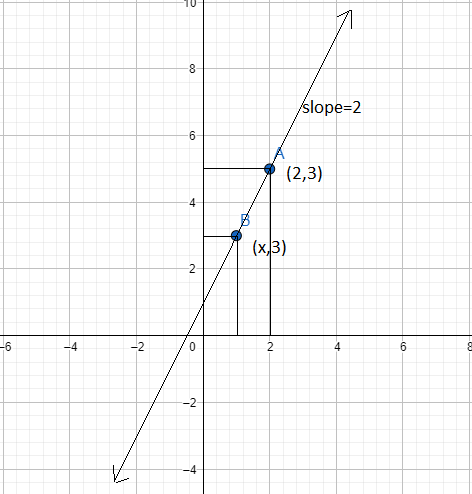
So we have ${{x}_{1}}=2,{{x}_{2}}=x,{{y}_{1}}=5,{{y}_{2}}=3$ and the slope if equal to 2.

& \Rightarrow slope=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}} \\\ & \Rightarrow 2=\dfrac{3-5}{x-2} \\\ & \Rightarrow 2=\dfrac{-2}{x-2} \\\ \end{aligned}$$ On cross multiplication we get as follows: $$\begin{aligned} & \Rightarrow 2(x-2)=-2 \\\ & \Rightarrow 2x-4=-2 \\\ \end{aligned}$$ On adding 4 to both the sides of the equality, we get as follows: $$\begin{aligned} & \Rightarrow 2x-4+4=-2+4 \\\ & \Rightarrow 2x=2 \\\ \end{aligned}$$ On dividing the equation on both sides by 2, we get as follows: $$\begin{aligned} & \Rightarrow \dfrac{2x}{2}=\dfrac{2}{2} \\\ & \Rightarrow x=1 \\\ \end{aligned}$$ Therefore, the value of x is equal to 1. Note: Substitute the values of $${{x}_{1}},{{x}_{2}},{{y}_{1}},{{y}_{2}}$$ in the formula very carefully because if you misplace its order then we will get a different value for x. Be careful not to use the formula with coordinates of x in the numerator instead of coordinates of y. Therefore, it is important to remember that the slope of a line is also equal to the tangent value of the angle made by the line and the x-axis in the anticlockwise direction with respect to x-axis.