Question
Question: If the roots of the equation $ax^3+bx^2-x+1=0$ are in H.P. then $\left|\frac{b_{max}}{a_{min}}\right...
If the roots of the equation ax3+bx2−x+1=0 are in H.P. then aminbmax equals ____.
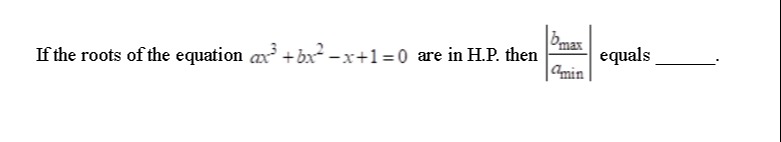
9
Solution
Solution:
Let the roots of
ax3+bx2−x+1=0be α, β, and γ in harmonic progression (H.P.). Then, the reciprocals α1, β1, γ1 are in arithmetic progression (A.P.), so
β1=21(α1+γ1)⟹2αγ=β(α+γ).From Vieta’s formulas for the cubic ax3+bx2−x+1=0:
- α+β+γ=−ab,
- αβ+βγ+γα=a−1,
- αβγ=−a1.
Since αβγ=−a1, we have
αγ=aβ−1.Also, from the sum we write:
α+γ=α+β+γ−β=−ab−β.Substitute into the H.P. condition:
2(aβ−1)=β(−ab−β).Multiply both sides by aβ (noting β=0):
−2=aβ2(−ab−β)=−bβ2−aβ3.Rearrange:
aβ3+bβ2−2=0.(1)But β is a root of the original cubic, so it satisfies:
aβ3+bβ2−β+1=0.(2)Subtract (1) from (2):
[aβ3+bβ2−β+1]−[aβ3+bβ2−2]=−β+3=0,which gives
β=3.Now substitute β=3 in equation (1):
a(27)+b(9)−2=0⟹27a+9b=2⟹b=92−27a.For the roots (other than β=3) to be real and distinct, consider the quadratic whose roots are α and γ. From Vieta for these two roots, using:
α+γ=−ab−3,αγ=3a−1.Their discriminant is:
Δ=(α+γ)2−4αγ=(−9a2)2−4(−3a1)=81a24+3a4=81a24+108a.For Δ>0, we require:
4+108a>0⟹a>−271.The ratio aminbmax is achieved when b is maximum and a is minimum. The expression b=92−3a shows that b is maximum when a is minimum (i.e. as low as possible). From the condition, the minimum possible a is just above −271; taking the infimum, we set:
amin=−271.Then,
bmax=92−27(−271)=92+1=93=31.Thus,
aminbmax=−27131=31×127=9.Minimal Explanation:
- For roots in H.P., reciprocals are in A.P. ⇒ 2αγ=β(α+γ).
- Using Vieta’s formulas and eliminating α, γ yields β=3 and 27a+9b−2=0.
- Express b as b=92−3a. For real distinct α and γ, a>−271.
- Minimum a is −271 giving maximum b=31.
- Hence, aminbmax=9.
