Question

If the resultant of two forces of magnitude $P$ and $2P$ is perpendicular to $P$, then the angle between the forces is
A. $\dfrac{{2\pi }}{3}$
B. $\dfrac{{3\pi }}{4}$
C. $\dfrac{{4\pi }}{5}$
D. $\dfrac{{5\pi }}{6}$

Answer 1

It is given in the above question that the resultant of the magnitude of two forces is perpendicular to $P$. So, by using the triangle law of vector addition, we have to draw the diagram. And then, by using trigonometric formulas, we will find the answer.

Complete step by step answer:
According to the given question, by using parallelogram law of vector addition we find the diagram as,

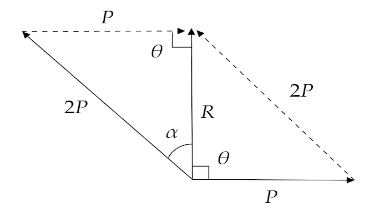
Let the resultant of the forces be $R$. As per the given question the angle between the resultant force $R$ and $P$ is $\theta = {90^ \circ }$.Now from the triangle to the left side of the figure we get,
$\sin \alpha = \dfrac{P}{{2P}}$
Eliminating $P$ from right side we get,
$\sin \alpha = \dfrac{1}{2} - - - - \left( 1 \right)$

From the value of trigonometric identities we know, $\sin {30^ \circ } = \dfrac{1}{2} - - - - - \left( 2 \right)$
So, by comparing equation $\left( 1 \right)$ with respect to equation $\left( 2 \right)$ we get,
$\alpha = {30^ \circ }$
Therefore, the angle between $P$ and $2P$ is,
$\left( {\alpha + \theta } \right) = {90^ \circ } + {30^ \circ } = {120^ \circ }$
Hence, the angle between the two forces is found to be ${120^ \circ }$.Now, ${120^ \circ }$ in the form of radian system is $\dfrac{{2\pi }}{3}$.

So, the correct option is A.

Additional information: The magnitude of resultant of two vectors $\overrightarrow P$ and $\overrightarrow Q$ is given as $R = \sqrt {{P^2} + {Q^2} + 2PQ\cos \theta }$ where $\theta$ is the angle between the two vectors $\overrightarrow P$ and $\overrightarrow Q$.

Note: It must be noted that we can also use the triangle law of vector addition to find the solution to this particular problem. In order to convert a degree system to a radian system we use the unitary method and the value of $\pi$ is considered to be ${180^ \circ }$.