Question

If the resultant of two forces is of magnitude $P$ and equal to one of them and perpendicular to it, then the other force is:
A. $P\sqrt 2$
B. $P$
C. $P\sqrt 3$
D. None of these

Answer 1

Here, clearly for the resultant vector to be perpendicular to one of the vectors the angle between the two initial vectors should be greater than $\dfrac{\pi }{2}$ as shown in the given figure. Now, to find the vector $\vec A$ we just need to write the formula for addition of the vectors $\vec A$ and $\vec B$ and the formula for the angle made by the resultant vector $\vec P$ with $\vec B$ . Solving the two equations simultaneously for $|A|$ and $\theta$ we get the magnitude of $\vec A$ .

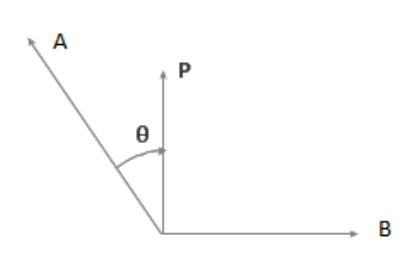
Complete step by step answer:
Vector addition forms the basis of 3-D geometry and all of classical mechanics. Here, according to the given question we have a resultant vector $\vec P$ which is equal in magnitude and perpendicular to one of the initial vectors $\vec B$. Since we know that $\vec P$ is the result of adding the vectors $\vec A$ and $\vec B$, we can thus express the magnitude of $\vec P$ as;
$|P|\, = \sqrt {{A^2} + {B^2} + 2AB\cos \theta }$

Squaring both the sides we get;
$|P{|^2} = \,|A{|^2} + |B{|^2} + 2|A||B|\cos \theta$
But according to the question, we have;
$|P|\, = \,|B|$
Therefore substituting the above $|P|$ with $|B|$ the equation could be re-written as;
$|P{|^2} = \,|A{|^2} + |P{|^2} + 2|A||B|\cos \theta \,\,\,\,\,$
Cancelling $|P|$from both sides and rearranging the equation we get;
$|A{|^2}\, = - 2|A||B|\cos \theta$
Cancelling $|A|$ out of the equation;
$|A|\, = - 2|B|\cos \theta$ …… (1)

Since we already know from the figure shown alongside that $\theta$ should be obtuse.Therefore at the end we have to make the correction for the ‘$-$ ’ sign in equation (1) by converting $\theta$ to $\pi - \theta$.According to the question we know that the angle between $\vec P$ and $\vec B$ is $\dfrac{\pi }{2}$. However by vector geometry we know that the angle made by the resultant vector and $\vec B$ could also is expressed as;
$\varphi = {\tan ^{ - 1}}\left( {\dfrac{{|A|\sin \theta }}{{|B| + |A|\cos \theta }}} \right)$

But, $\varphi = \dfrac{\pi }{2}$ . Therefore;
$\dfrac{\pi }{2} = {\tan ^{ - 1}}\left( {\dfrac{{|A|\sin \theta }}{{|B| + |A|\cos \theta }}} \right)$ …… (2)
Thus, we have two equations (2) and (3) and two variables $|A|$ and $\theta$. Substituting the values of (2) in (3) we get the equation;
$\dfrac{\pi }{2} = {\tan ^{ - 1}}\left( {\dfrac{{ - 2|B|\cos \left( \theta \right)\sin (\theta )}}{{|B| - \,2|B|{{\cos }^2}\left( \theta \right)}}} \right)$
Using trigonometric identities for double angle of sine and cosine, we can simplify the equations to be;
$\dfrac{\pi }{2} = {\tan ^{ - 1}}\left( {\dfrac{{ - |B|\sin (2\theta )}}{{ - |B|\left( {\cos \left( {2\theta } \right)} \right)\,}}} \right)$

Cancelling $|B|$ out of the equation, the equation simplifies to;
$\dfrac{\pi }{2} = {\tan ^{ - 1}}\left( {\dfrac{{\sin (2\theta )}}{{\cos \left( {2\theta } \right)\,}}} \right)$
$\dfrac{\pi }{2} = {\tan ^{ - 1}}\left( {\tan 2\theta } \right)$
Since; ${\tan ^{ - 1}}\left( {\tan \left( x \right)} \right) = x$ , therefore;
${\tan ^{ - 1}}\left( {\tan 2\theta } \right) = 2\theta$
$\Rightarrow \dfrac{\pi }{2} = 2\theta$

But accounting for the correction for the obtuse angle;
$\dfrac{\pi }{2} = 2\left( {\pi - \theta } \right)$
On solving, we get;
$\theta = \dfrac{{3\pi }}{4}$ …… (3)
Substituting the value of (3) in (1) we get;
$|A|\, = - 2|P|\cos \left( {\dfrac{{3\pi }}{4}} \right) \\\ \Rightarrow |A|\, = - 2|P|\left( { - \dfrac{1}{{\sqrt 2 }}} \right) \\\ \therefore |A|\, = \sqrt 2 P \\\$

Hence option A is correct.

Note: The vector addition for two vectors can be done by either triangle law of vector addition or parallelogram law of vector addition and more than two vectors are added by polygon law of vector addition. When head and tail join together then triangle law of vector addition and when same -same point are touched then parallelogram law is used.