Question

If the resultant of $3\overrightarrow{p}$ and $4\overrightarrow{p}$ is a force $5\overrightarrow{p}$, then the angle between $3\overrightarrow{p}$ and $5\overrightarrow{p}$ is
a. ${{\sin }^{-1}}\left( \dfrac{3}{5} \right)$
b. ${{\sin }^{-1}}\left( \dfrac{4}{5} \right)$
c. ${{90}^{\circ }}$
d. None of these

Answer 1

First we will put the values in the resultant formula. Now using this we will find the angle made between the resultant and the forces $3\overrightarrow{p}$ and $5\overrightarrow{p}$. Take angle between $4\overrightarrow{p}$ and $5\overrightarrow{p}$ as $\beta$, $\alpha$ between $5\overrightarrow{p}$ and $3\overrightarrow{p}$. So, we have the total angle $\phi =\alpha +\beta$.

Complete step by step answer:
Now consider the figure drawn below,

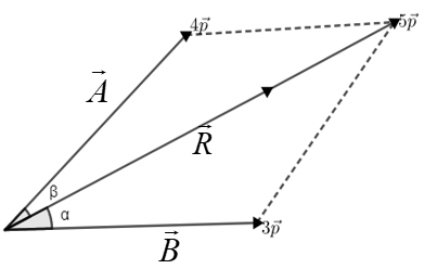
Now the force $4\overrightarrow{p}$ and force $3\overrightarrow{p}$ is drawn and the resultant of these two forces is $5\overrightarrow{p}$ force.
Let the angle made between the $4\overrightarrow{p}$ force and resultant $5\overrightarrow{p}$ is $\beta$ and the angle made between the $3\overrightarrow{p}$ force and resultant $5\overrightarrow{p}$ is $\alpha$.
We know the basic formula where the resultant between 2 vectors $\overrightarrow{A}$ and $\overrightarrow{B}$ is given by the equation,
${{R}^{2}}={{A}^{2}}+{{B}^{2}}+2AB\cos \phi$
Let us substitute the value into the equation, Hence we havr resultant $=R=5\overrightarrow{p}$ $A=4\overrightarrow{p}$ and $B=3\overrightarrow{p}$
Put ,$\phi =\alpha +\beta$ in the above expression.

& \Rightarrow {{\left( 5\overrightarrow{p} \right)}^{2}}={{\left( 4\overrightarrow{p} \right)}^{2}}+{{\left( 3\overrightarrow{p} \right)}^{2}}+2\left( 4\overrightarrow{p} \right)\left( 3\overrightarrow{p} \right)\cos \left( \alpha +\beta \right) \\\ & \Rightarrow 25{{\overrightarrow{p}}^{2}}=16{{\overrightarrow{p}}^{2}}+9{{\overrightarrow{p}}^{2}}+24{{\overrightarrow{p}}^{2}}\cos \left( \alpha +\beta \right) \\\ & 25{{\overrightarrow{p}}^{2}}=25{{\overrightarrow{p}}^{2}}+24{{\overrightarrow{p}}^{2}}\cos \left( \alpha +\beta \right) \\\ \end{aligned}$$ Cancel out $$25{{\overrightarrow{p}}^{2}}$$ from LHS and RHS. $$\begin{aligned} & \Rightarrow 24{{\overrightarrow{p}}^{2}}\cos \left( \alpha +\beta \right)=0 \\\ & \cos \left( \alpha +\beta \right)=0 \\\ & \Rightarrow \alpha +\beta ={{\cos }^{-1}}0\left[ \because {{\cos }^{-1}}0={{90}^{\circ }} \right] \\\ & \alpha +\beta ={{90}^{\circ }} \\\ \end{aligned}$$ Now, from the figure we can use the sine function to bring out the relation between the resultant and the vectors using the below mentioned formula. Now we can say that $\vec{R}\sin \alpha =\vec{B}\sin \left( \alpha +\beta \right)$ which is nothing but y projection of $\vec{B}$ and $\vec{R}$. Hence we have $$\overrightarrow{B}=\dfrac{\overrightarrow{R}\sin \alpha }{\sin \left( \alpha +\beta \right)}$$ Now substituting the values of $$\overrightarrow{A}=4\overrightarrow{p},\overrightarrow{B}=3\overrightarrow{p},\alpha +\beta ={{90}^{\circ }},\overrightarrow{R}=5\overrightarrow{p}$$ we get, $$\begin{aligned} & \Rightarrow 4\overrightarrow{p}=\dfrac{5\overrightarrow{p}\sin \alpha }{\sin 90}\left[ \because \sin 90=1 \right] \\\ & \Rightarrow 4\overrightarrow{p}=\dfrac{5\overrightarrow{p}\sin \alpha }{1} \\\ & \sin \alpha =\dfrac{4\overrightarrow{p}}{5\overrightarrow{p}} \\\ & \Rightarrow \sin \alpha =\dfrac{4}{5} \\\ & \therefore \alpha ={{\sin }^{-1}}\left( \dfrac{4}{5} \right) \\\ \end{aligned}$$ **So, the correct answer is “Option b”.** **Note:** The angle between the resultants is taken as $$\alpha $$ and $$\beta $$, which makes the total angle $$\phi =\alpha +\beta $$. We can solve this in easy way by directly applying the formula, $$\overrightarrow{B}=\dfrac{\overrightarrow{R}\sin \alpha }{\sin \left( \alpha +\beta \right)}$$.