Question
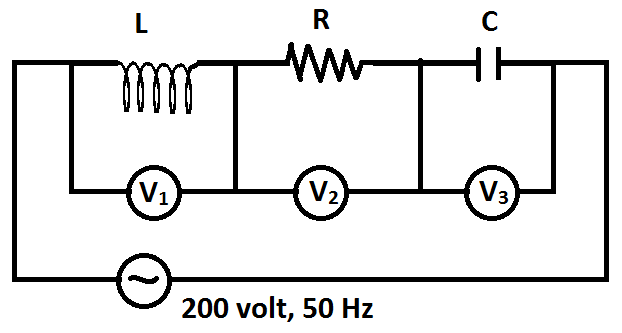
Question: If the readings \( {V_1} \) and \( {V_3} \) are \( 100volt \) , each then reading of \( {V_2} \) is:...
If the readings V1 and V3 are 100volt , each then reading of V2 is:
(A) 0volt
(B) 100volt
(C) 200volt
(D) Cannot be determined by given information
Solution
Hint : Here, we are given the LRC circuit. We can see that the inductor, the resistor and the capacitor are connected in series connection here. In series connection, the current flowing through all the elements will be the same but the voltage across each element is different. We will use the formula for total voltage in the series connection for LRC circuit to find the required answer.
V=VR2+(VL−VC)2 , Where, V is the total voltage supply, VR is the voltage across the resistor, VL is the voltage across the inductor and VC is the voltage across the capacitor.
Complete Step By Step Answer:
From the given figure, we can see that V1 is the voltage across the inductor, V2 is the voltage across the resistor and V3 is the voltage across the capacitor. Therefore if we use the formula V=VR2+(VL−VC)2 for the given case , we will get
V=V22+(V1−V3)2
From the given data, we can write that V=200volt and V1=V3=100volt .
Now, we will put these values in the equation.
⇒200=V22+(100−100)2=V2 ⇒V2=100volt
Thus, the voltage across the resistor in the given case is 200volt .
Hence, option C is the right answer.
Note :
In this question, we have used the formula for the total voltage in the series connection of an RLC circuit. We have seen that when the voltage across the inductor and the voltage across the capacitor is same, the voltage across the resistor will be same as the total voltage supply. It is also important to remember that in this series connection of an RLC circuit, the current flowing through all the components is the same.
