Question
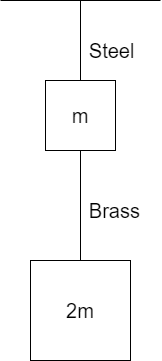
Question: If the ratio of lengths, radii and Young's modulus of steel and brass wires in the figure are a,b an...
If the ratio of lengths, radii and Young's modulus of steel and brass wires in the figure are a,b and c respectively, then the corresponding is:
A) b2a2c
B) 2b2c3a
C) b22ac
D) 2ab23c
Solution
Recall that Young’s modulus is the mechanical property of a material such that it can withstand the stretching or contraction with respect to the length. The value of Young’s modulus is most commonly used. It describes the relation between stress and strain.
Complete step by step solution:
Step I: The formula for Young’s modulus for a material is given by the formula
ΔL=AYFL
Where ‘F’ is the force applied
‘L’ is the length
‘A’ is the area
‘Y’ is the Young’s modulus of elasticity
Step II: Given that ratio of length, radii and Young’s modulus is a, b and c. The force on the steel wire will be due to both the masses and the force of gravity acting downwards. Therefore,
⇒Fs=(m+2m)g=3mg
The Young’s modulus due to steel is given by
ΔLs=AYsFLs
⇒ΔLs=πrs2×Ys3mg×Ls---(i)
Step III: Similarly, the force on brass wire will only be due to mass ‘2m’. The Young’s modulus due to brass wire is given by
⇒ΔLB=πrB2×YB2mg×LB---(ii)
Step IV: The ratio of steel and brass wires can be written using equation (i) and equation (ii)
⇒ΔLBΔLS=πrB2×YB2mg×LBπrS2×YS3mg×LS
⇒ΔLBΔLS=2mg×LB×πrS2×YS3mg×LS×πrB2×YB
⇒ΔLBΔLS=2b2c3a
Option B is the right answer.
Note: It is important to note that if the Young’s modulus of a substance is known then it can be known whether the substance is rigid or not and to what extent. By knowing, the rigidity of a substance, its tendency to experience the change in its shape can be known. In other words, it determines the effect of applied force on the shape of a certain substance.
